0.10 Sets and counting  (Page 6/9)

Clearly, this makes sense. For every permutation of three math books placed in the first three slots, there are $5P2$ permutations of history books that can be placed in the last two slots. Hence the multiplication axiom applies, and we have the answer $\left(4P3\right)\left(5P2\right)$ .

We summarize.

1. Permutations

   A permutation of a set of elements is an ordered arrangement where each element is used once.

2. Factorial

   $n!=n\left(n-1\right)\left(n-2\right)\left(n-3\right)\cdots 3\cdot 2\cdot 1$ .

   Where $n$ is a natural number.

   $0!=1$
3. Permutations of $n$ Objects Taken $r$ at a Time

   $n\text{Pr}=n\left(n-1\right)\left(n-2\right)\left(n-3\right)\cdots \left(n-r+1\right)$ , or $n\text{Pr}=\frac{n!}{\left(n-r\right)!}$

   Where $n$ and $r$ are natural numbers.

Circular permutations and permutations with similar elements

Section overview

In this section we will address the following two problems.

1. In how many different ways can five people be seated in a circle?
2. In how many different ways can the letters of the word MISSISSIPPI be arranged?

The first problem comes under the category of Circular Permutations, and the second under Permutations with Similar Elements.

Circular permutations

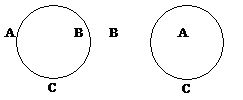
It happens that there are only two ways we can seat three people in a circle. This kind of permutation is called a circular permutation. In such cases, no matter where the first person sits, the permutation is not affected. Each person can shift as many places as they like, and the permutation will not be changed. Imagine the people on a merry-go-round; the rotation of the permutation does not generate a new permutation. So in circular permutations, the first person is considered a place holder, and where he sits does not matter.