| << Chapter < Page | Chapter >> Page > |
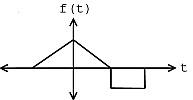
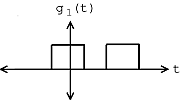
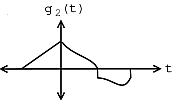
For example, consider the target signal given in [link] and the set of two signals given in [link] . By inspection, it is clear that the signal is most like the target signal . However, to make that conclusion mathematically, we use the matched filter detector with the inner product. If we were to actually make the necessary computations, we would first normalize each signal and then compute the necessary inner products in order to compare the signals in with the target signal . We would notice that the absolute value of the inner product for with when normalized is greater than the absolute value of the inner product of with when normalized, mathematically stated as
A somewhat more involved matched filter detector scheme would involve attempting to match a target time limited signal to a set of of time shifted and windowed versions of a single signal indexed by . The windowing funtion is given by where is the interval to which is time limited. This scheme could be used to find portions of that have the same shape as . If the absolute value of the inner product of the normalized versions of and is large, which is the absolute value of the normalized correlation for standard inner products, then has a high degree of “likeness” to on the interval to which is time limited but left shifted by . Of course, if is not time limited, it means that the entire signal has a high degree of “likeness” to left shifted by .
Thus, in order to determine the most likely locations of a signal with the same shape as the target signal in a signal we wish to compute
to provide the desired shift. Assuming the inner product space examined is (similar results hold for , , and ), this produces
Since and are time limited to the same interval
Making the subsitution ,
Noting that this expression contains a convolution operation
where is the conjugate of the time reversed version of defined by
In the special case in which the target signal is not time limited, has unit value on the entire real line. Thus, the norm can be evaluated as . Therefore, the function reduces to where The function is known as the normalized cross-correlation of and .
Hence, this matched filter scheme can be implemented as a convolution. Therefore, it may be expedient to implement it in the frequency domain. Similar results hold for the , , and spaces. It is especially useful to implement the cases in the frequency domain as the power of the Fast Fourier Transform algorithm can be leveraged to quickly perform the computations in a computer program. In the and cases, care must be taken to zero pad the signal if wrap-around effects are not desired. Similar results also hold for spaces on higher dimensional intervals with the same inner products.
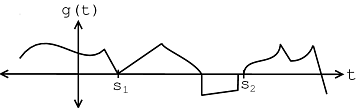
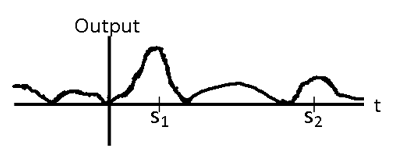
Of course, there is not necessarily exactly one instance of a target signal in a given signal. There could be one instance, more than one instance, or no instance of a target signal. Therefore, it is often more practical to identify all shifts corresponding to local maxima that are above a certain threshold.
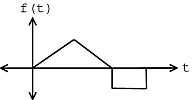
The signal in [link] contains an instance of the template signal seen in [link] beginning at time as shown by the plot in [link] . Therefore,
Proof of the cauchy-schwarz inequality
As can be seen, the Cauchy-Schwarz inequality is a property of inner product spaces over real or complex fields that is of particular importance to the study of signals. Specifically, the implication that the absolute value of an inner product is maximized over normal vectors when the two arguments are linearly dependent is key to the justification of the matched filter detector. Thus, it enables the use of matched filters for such pattern matching applications as image detection, communications demodulation, and radar signal analysis.

Notification Switch
Would you like to follow the 'Signals and systems' conversation and receive update notifications?