| << Chapter < Page | Chapter >> Page > |
-23,450 23,450
Góc lệch có thể tính toán theo phương trình của Cooper:
= 23,45.sin(360 )
trong đó n là thứ tự ngày của 1 năm .
Quan hệ giữa các loại góc đặc trưng ở trên có thể biểu diễn bằng phương trình giữa góc tới và các góc khác như sau:
cos = sin.sin. cos - sin.cos. sin.cos + cos.cos.cos.cos +
+ cos.sin.sin.cos.cos + cos.sin.sin.sin
và:cos = cosz.cos + sinz.sin.cos(s - )
Đối với bề mặt nằm ngang góc tới chính là góc thiên đỉnh của mặt trời z, giá trị của nó phải nằm trong khoảng 00 và 900 từ khi mặt trời mọc đến khi mặt trời ở thiên đỉnh ( = 0):
cosz = cos.cos.cos + sin.sin
Tại thời điểm bất kỳ, bức xạ mặt trời đến một bề mặt nằm ngang ngoài khí quyển được xác định theo phương trình:
Thay giá trị cosz vào phương trình trên ta có Eo.ng tại thời điểm bất kỳ từ lúc mặt trời mọc đến lúc mặt trời lặn:
Tích phân phương trình này theo thời gian từ khi mặt trời mọc đến khi mặt trời lặn (6h đến 18h mặt trời) ta sẽ được Eo. ngay là năng lượng bức xạ mặt trời trên mặt phẳng nằm ngang trong một ngày:
với s là góc giờ mặt trời lặn (0) (tức là góc giờ khi z = 900)
Người ta cũng xác định năng lượng bức xạ ngày trung bình tháng Eoth bằng cách thay giá trị n và trong các công thức trên lấy bằng giá trị ngày trung bình của tháng và độ lệch tương ứng.
Năng lượng bức xạ trên mặt phẳng nằm ngang trong một giờ nhất định có thể xác định khi phân tích phương trình 1.9 trong khoảng thời gian giữa các góc giờ 1 và 2:
Tổng bức xạ mặt trời lên một bề mặt đặt trên mặt đất bao gồm hai phần chính đó là trực xạ và tán xạ. Phần trực xạ đã đựơc khảo sát ở trên, còn thành phần tán xạ thì khá phức tạp. Hướng của bức xạ khuếch tán truyền tới bề mặt là hàm số của độ mây và độ trong suốt của khí quyển, các đại lượng này lại thay đổi khá nhiều. Có thể xem bức xạ tán xạ là tổng hợp của 3 thành phần (hình 2.6).
- Thành phần tán xạ đẳng hướng: phần tán xạ nhận được đồng đều từ toàn bộ vòm trời.
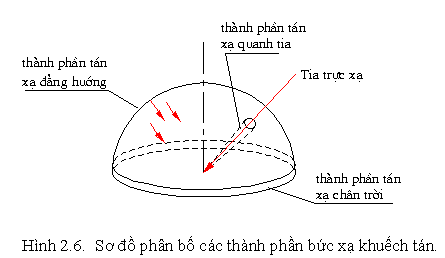
Góc khuếch tán ở mức độ nhất định phụ thuộc độ phản xạ Rg (còn gọi là albedo -suất phân chiếu) của mặt đất. Những bề mặt có độ phản xạ cao (ví dụ bề mặt tuyết xốp có Rg = 0,7) sẽ phản xạ mạnh bức xạ mặt trời trở lại bầu trời và lần lượt bị phát tán trở thành thành phần tán xạ chân trời.
Như vậy bức xạ mặt trời truyền đến một bề mặt nghiêng là tổng của các dòng bức xạ bao gồm: trực xạ Eb, 3 thành phần tán xạ Ed1, Ed2, Ed3 và bức xạ phản xạ từ các bề mặt khác lân cận Er:
E = Eb + Ed1 + Ed2 + Ed3 + Er
Tuy nhiên việc tính toán các đại lượng tán xạ này rất phức tạp. Vì vậy người ta giả thiết là sự kết hợp của bức xạ khuếch tán và bức xạ phản xạ của mặt đất là đẳng hướng, nghĩa là tổng của bức xạ khuếch tán từ bầu trời và bức xạ phản xạ của mặt đất là như nhau trong mọi trường hợp không phụ thuộc hướng của bề mặt. Như vậy tổng xạ trên bề mặt nghiêng sẽ là tổng của trực xạ Eb.Bb và tán xạ trên mặt nằm ngang Ed.

Notification Switch
Would you like to follow the 'Năng lượng mặt trời- lý thuyết và ứng dụng' conversation and receive update notifications?