| << Chapter < Page | Chapter >> Page > |
Nou kan jy enige vraag rakende ‘n sirkel of wiel of enigiets wat rond is beantwoord, as dit met middellyn, radius en omtrek te doen het.
5. Gebruik jou sakrekenaar om die omtrek van elk van die volgende sirkels te bereken:
Belangrik : Skryf altyd eers die formule neer.(π = 3,14).
5.1 r = 230 mm 5.2
r = 1,45 cm (antwoord tot tweedes)
6. Bepaal die omtrek van elk van die volgende sirkels sonder die gebruik van ‘n sakrekenaar.
Belangrik : Skryf eers die formule neer.(π = 22/7)
6.1 r = 14 cm
6.2 d = 35 cm
7. Bereken die radius van die volgende sirkel: Jy mag jou sakrekenaar gebruik, maar jy moet alle stappe toon. (π= 22/7)
7.1 omtrek 242 mm
8. Hoeveel omwentelings sal ‘n bergfietswiel met middellyn van 67 cm maak oor ‘n afstand van 7,5 m?
AKTIWITEIT 3
Om die oppervlakte van ‘n sirkel te ontdek en probleme in dié verband te bemeester
| LU 4.2.1 | LU 4.2.1 | LU 4.5.1 | LU 4.3 |
1. Kan jy nog onthou wat die formule is om die oppervlakte van ‘n reghoek te bereken?
2. Trek ‘n sirkel met middelpunt O met radius 60 mm op ‘n vel papier. Verdeel die sirkel in 32 ewe groot sektore. Kleur 16 rooi in en die ander 16 blou.
3. Knip nou al 32 sektore uit en plaas hulle langs mekaar, sodat die driehoeke ‘n plaveisel vorm om uiteindelik ‘n reghoek te vorm.
4. Meet nou die lengte en breedte van die reghoek. Bereken nou met behulp van die formule in nr. 1 die oppervlakte van jou reghoek.
5. Watter afleiding kan jy maak ten opsigte van die reghoek en die sirkel wat jy in nr. 2 geteken het?
6. In watter eenhede word oppervlakte bereken?
7. Gee nou ‘n formule om die oppervlakte van enige sirkel te bereken.
8. Bereken nou die oppervlakte van die sirkel wat jy in nr. 2 gekonstrueer het met behulp van die formule in nr. 7.
Wat sien jy?
9. Bereken die oppervlakte van die volgende sirkels sonder ‘n sakrekenaar.
9.1 r = 14,7 cm
9.2 d = 56,49 cm
10. Bereken die oppervlakte van die gearseerde gedeeltes.
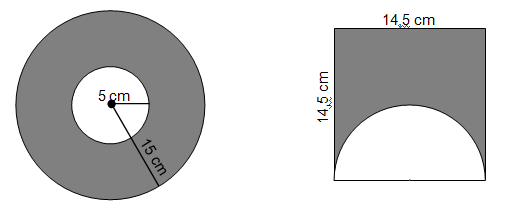
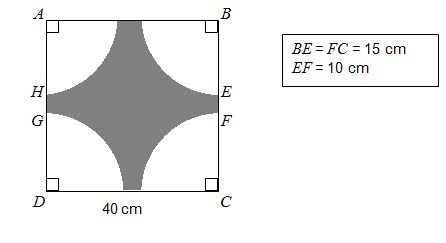
11. Bereken die oppervlakte van die gearseerde gedeeltes.
| LU 3 |
| Ruimte en Vorm (Meetkunde)Die leerder is in staat om eienskappe van en verwantskappe tussen twee- dimensionele vorms en drie-dimensionele voorwerpe in ’n verskeidenheid oriënta-sies en posisies te beskryf en voor te stel. |
| Dit word bewys as die leerder: |
| 3.2 in kontekste insluitend sodaniges wat gebruik kan word om bewustheid van sosiale, kulturele en omgewingsaangeleenthede te skep, geometriese figure en soliedes kan beskryf en klassifiseer in terme van eienskappe, insluitend: |
| 3.2.1 sye, hoeke en diagonale en hul verbande, met die fokus op driehoeke en kwadrilaterale (bv. tipes driehoeke en kwadrilaterale). |
| LU 4 |
| MetingDie leerder is in staat om gepaste meeteenhede, -instrumente en formules in ’n verskeidenheid kontekste te gebruik. |
| Dit word bewys as die leerder: |
| 4.2 probleme kan oplos wat die volgende behels: |
| 4.2.1 lengte; |
| 4.2.2 omtrek en oppervlak van poligone en sirkels; |
| 4.3 probleme aan die hand van ‘n reeks strategieë oplos wat die volgende insluit: |
| 4.3.1 skatting; |
| 4.3.2 berekening tot minstens twee desimale plekke; |
| 4.3.3 die gebruik en omskakeling van toepaslike SI eenhede; |
| 4.4 die betekenis van kan beskryf en dit in berekeninge wat sirkels behels kan gebruik, en ook die historiese ontwikkeling daarvan in meting kan bespreek; |
| 4.5 die volgende kan bereken deur toepaslike formules te kies en te gebruik: |
| 4.5.1 omtrek van poligone en sirkels; |
| 4.5.2 oppervlakte van driehoeke, reghoeke, sirkels en poligone deur hulle in driehoeke en reghoeke op te breek; |
| 4.8 die verband tussen die sye van ‘n reghoekige driehoek kan ondersoek (alleen en/of as lid van ‘n groep) om die stelling van Pythagoras te ondersoek; |
| 4.9 die stelling van Pythagoras kan gebruik om ‘n ontbrekende lengte in ‘n reghoekige driehoek te bereken terwyl irrasionele antwoorde in surd-vorm (√) gelaat word; |
| 4.10 wyses van meting in verskillende kulture in die geskiedenis kan beskryf en illustreer (bv. die bepaling van reghoeke deur geknoopte lyn te gebruik en by die stelling van Pythagoras uit te kom). |
AKTIWITEIT 2
5.1 O = x d
O = x 460
O = 1 444,4 mm
5.2 C = x d
C = x 2,9
C 9,11 cm
6.1 C = x d
C = x
C = 88 cm
6.2 C = x d
C = x
C = 110 cm
7.1 C = x d
242 = x d
x = d
d = 77 mm
8. C = x d
= 3,14 x 67 cm
= 210,38 cm
750 ÷ 210,38 cm
= 3,6 rewolusies
AKTIWITEIT 3
9. A = x r 2
= x x
= 679,14 cm 2
A = 2 505,92 cm 2
10. A
(3,14 x 15 2 ) – (3,14 x 15 2 )
= 706,5 – 78,5
= 628 cm 2
B
(14,5) 2 – (3,14 x 7,25 2 x )
= 210,25 – 82,52
= 127,73 cm 2
11. (40 x 40) – (3,14 x 15 2 )
= 1 600 – 706,5
= 893,5 cm 2

Notification Switch
Would you like to follow the 'Wiskunde graad 8' conversation and receive update notifications?