| << Chapter < Page | Chapter >> Page > |
3.3 As jy slegs die inligting, soos in die sketse hieronder, kry, sal jy met sekerheid kan sê dat die twee driehoeke altyd kongruent is?
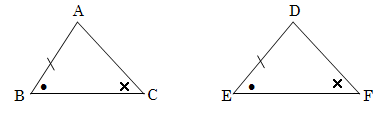
3.4 Sal die volgende driehoeke altyd kongruent wees? Hoekom sê jy so?

4.1 Kyk na bladsy A-4 van die akkuraat gekonstrueerde driehoeke. Al die driehoeke op bladsy A-4 is gekonstrueer deurdat die twee sye en die hoek nie tussen die gegewe sye (ss ) gebruik is om die driehoeke te konstrueer nie. Soek al die pare driehoeke wat kongruent is en skryf hulle neer in volgorde van die elemente wat gelyk is.
4.2 Daar is twee driehoeke wat, hoewel die twee sye en die hoek gelyk is, nie kongruent is nie. Noem hulle.
4.3.1 Dink jy dat, as twee sye en die nie-ingeslote hoek gegee word, die driehoeke wat só gekonstrueer word altyd kongruent sal wees?
4.3.2 Aan watter vereiste moet die lengtes van die twee sye wat gebruik word om die driehoeke te konstrueer, voldoen vir die driehoeke om kongruent te wees?
4.4.4 As jy slegs die inligting, soos in die sketse hieronder, kry, sal jy met sekerheid kan sê dat die twee driehoeke altyd kongruent is? (Onthou, jy weet nie nou hoe lank die twee gegewe sye is nie).
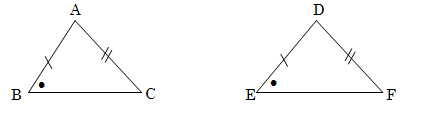
4.5.1 Daar is vier driehoeke op bladsy A-4 waar die gegewe hoek 90° is. As die nie-ingeslote hoek 90° is, dink jy dat die twee driehoeke altyd kongruent sal wees? (s s 90 ° )
4.5.2 As jy slegs die inligting, soos in die sketse hieronder, kry, sal jy met sekerheid kan sê dat die twee driehoeke altyd kongruent is?
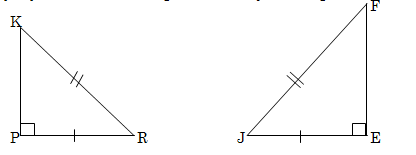
5. Op bladsy A-5 kry jy driehoeke waarvan die drie hoeke van die een driehoek gelyk is aan die drie hoeke van die ander driehoek. ( )
5.1 Is driehoeke wat só gekonstrueer word , noodwendig altyd kongruent?
5.2 As jy slegs die inligting, soos in die sketse hieronder, kry, sal jy met sekerheid kan sê dat die twee driehoeke altyd kongruent is?
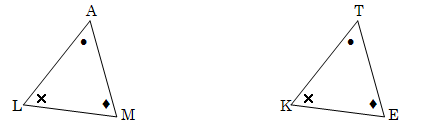
6. Gee nou self die kombinasies van sye en hoeke vir driehoeke om kongruent te wees. Illustreer elke kombinasie soos die voorbeeld hieronder:
1.
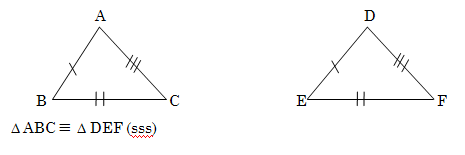
2.
3.
4.
Huiswerkopdrag
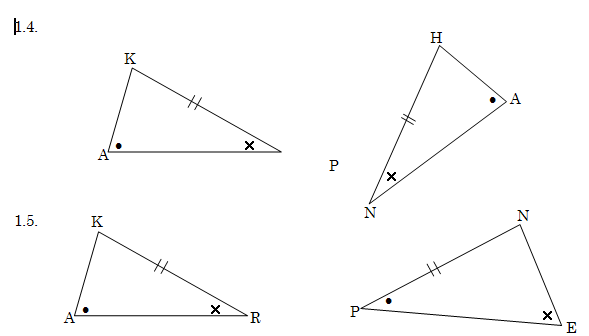
1. Sê of die volgende pare driehoek kongruent is of nie. Doen elke nommer soos die voorbeeld hieronder.
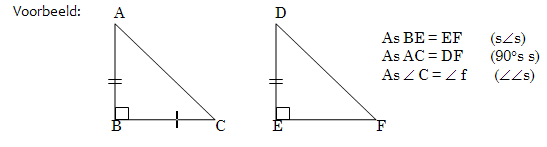
Voorbeeld:
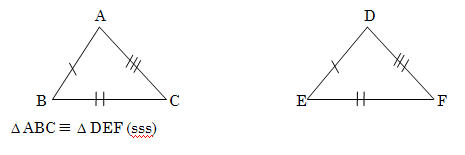
Δ ABC Δ DEF (sss) A = D; B = E en C = F
L.W. As die driehoeke nie noodwendig kongruent is nie, skryf dan ΔABC ΔDEF en skryf dan neer hoekom jy so sê.
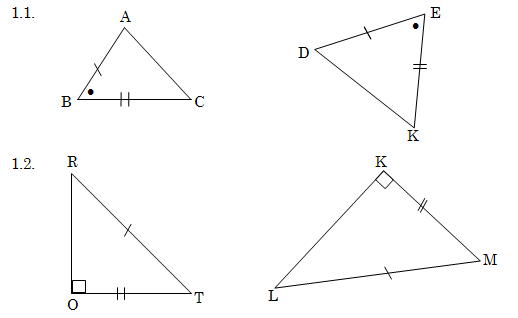
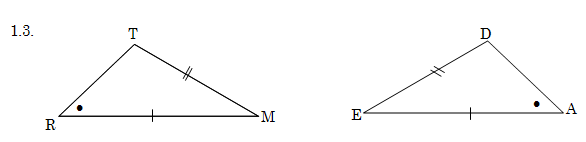
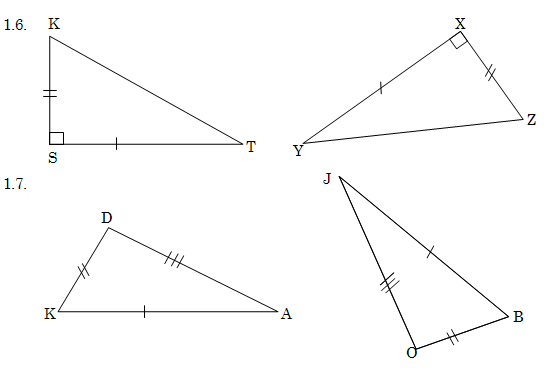
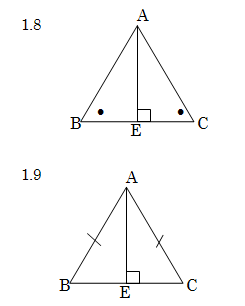
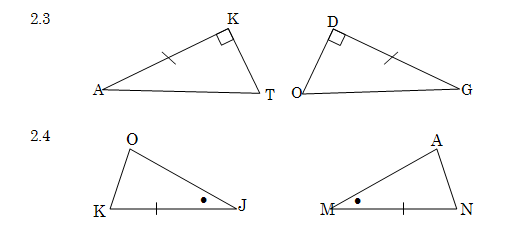
2. In elk van die volgende pare driehoeke is twee pare dele gelyk gemaak. Skryf in elke geval nog ‘n paar dele neer wat gelyk moet wees om kongruensie te verseker. Gee die kongruensietoets wat jy gebruik en gee ook al die moontlikhede sonder om een kongruensietoets te herhaal.
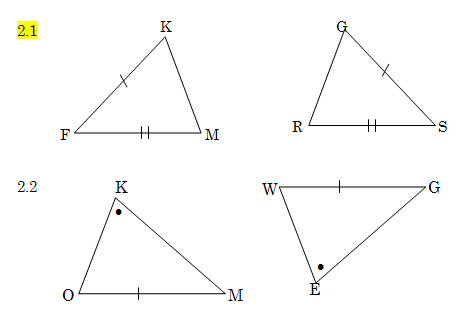
Assessering
| LU 3 |
| Ruimte en Vorm (Meetkunde)Die leerder is in staat om eienskappe van en verwantskappe tussen tweedimensionele vorms en driedimensionele voorwerpe in ‘n verskeidenheid oriëntasies en posisies te beskryf en voor te stel. |
| Ons weet dit as die leerder: |
| 3.1 meetkundige figure en driedimensionele voorwerpe in natuurlike en kulturele vorms en meetkundige agtergrond herken, visualiseer en benoem, insluitend: |
| 3.1.1 reëlmatige en onreëlmatige veelhoeke en veelvlakke; |
| 3.1.2 sfere; |
| 3.1.3 silinders; |
| 3.2 die onderlinge verwantskappe van meetkundige figure en driedimensionele voorwerpe se eienskappe met bewyse in kontekste, insluitend dié wat gebruik kan word om ‘n bewustheid van sosiale, kulturele en omgewingsake te bevorder beskryf, insluitend:3.2.1 kongruensie en reguitlynmeetkunde; |

Notification Switch
Would you like to follow the 'Wiskunde graad 9' conversation and receive update notifications?