| << Chapter < Page | Chapter >> Page > |
Ons sien dus dat by driehoeke net een van die voorwaardes vir gelykvormigheid teenwoordig hoef te wees.
Dit beteken as drie hoeke van die een driehoek gelyk is aan drie hoeke van die ander driehoek, dan is die sye in dieselfde verhouding en dus is die twee driehoeke gelykvormig.
Dit beteken ook dat, as die ooreenkomstige sye van die twee driehoeke in dieselfde verhouding is, dan is die ooreenkomstige hoeke van die twee driehoeke gelyk en dus is die twee driehoeke gelykvormig.
Huiswerkopdrag
1. Die volgende pare driehoeke word gegee. Sê of hulle gelykvormig is of nie en gee redes vir jou antwoord. As die paar driehoeke gelykvormig is, bereken die groottes van die sye en die hoeke wat nie in die figure gegee is nie.
Voorbeeld:
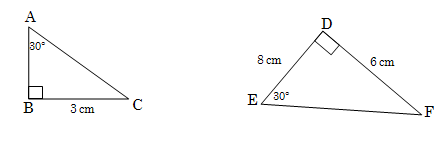
C = F = 60°Δ ABC ΔEDF ()
AB = 4 cmAC = 5 cm (pyth)EF = 10 cm
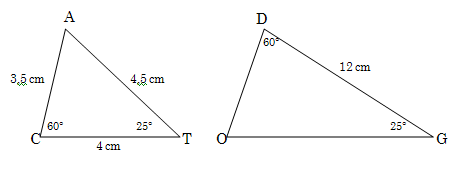
1.1.
1.2
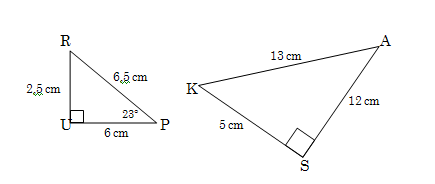
1.3
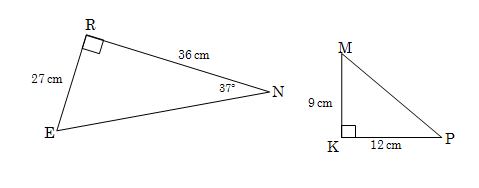
1.4
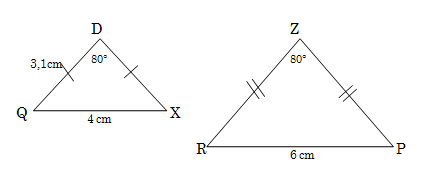
2.
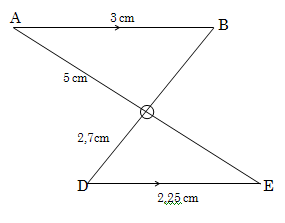
2.1 Voltooi die volgende:
In ΔAOB en ΔDOE:
Rede
.......... = .......... (...........................................................................)
.......... = .......... (...........................................................................)
Δ.............. .............. ( )
2.2 Bereken nou die lengtes van die ontbrekende sye.
3. In die figuur is FH = 12 cm.
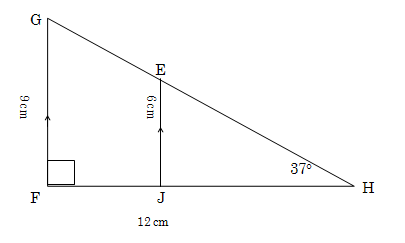
3.1 Voltooi die volgende:
In Δ.......... en Δ..........
.......... = .......... (...........................................................................)
.......... = .......... (...........................................................................)
Δ.............. .............. ( )
3.2 Bereken nou die lengtes van die volgende:
3.2.1 HE
3.2.2 EG
3.2.3 FJ
4. Die hoogte van ‘n hoë, vertikale voorwerp word bepaal deurdat die skaduwee van ‘n stok van bekende lengte gemeet word en die skaduwee van die voorwerp gemeet word. Die volgende figure gee die metings wat gemaak is.
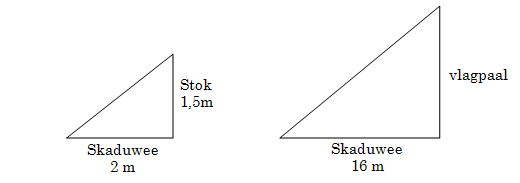
Bepaal die lengte van die vlagpaal
ASSESSERINGSTAAK:
Om van gelykvormigheid gebruik te maak om die hoogte van ‘n hoë voorwerp te meet:
Werk in pare saam.
1. Die volgende word benodig:
‘n Maatband van tenminste 5 m lank
‘n Spieël
‘n Liniaal
‘n Veltpen
2. Gaan soos volg te werk:
Soek twee hoë, vertikale voorwerpe op die skoolgrond soos byvoorbeeld ‘n netbalpaal, ‘n lamppaal, rugbypale of ‘n vlagpaal. Soek veral voorwerpe waarvan die hoogte normaalweg moeilik fisies gemeet kan word.
Trek twee dun lyne met die veltpen op die spieël sodat die lyne mekaar loodreg kruis.
Plaas nou die spieël op gelyk grond ‘n ent vanaf die hoë voorwerp.
Een persoon staan nou terug en kyk in die spieël en verskuif sy / haar posisie totdat die top van die voorwerp presies op die snypunt van die twee lyne op die spieël val.
3. Meet die volgende:
die hoogte van die persoon wat in die spieël gekyk het tot by sy/ haar oë
die afstand tussen die persoon wat in die spieël gekyk het en die snypunt van die lyne in die spieël
die afstand tussen die voorwerp en die snypunt van die lyne in die spieël.
Resultate:
1. Teken die tabel oor op ‘n foliobladsy en voltooi dit:
| Die voorwerp waarvan die hoogte gemeet word | Ooghoogte van die persoon | Afstand tussen die persoon en die snypunt van die lyne op die spieël | Afstand vanaf die spieël tot by die voorwerp | Berekende hoogte van die voorwerp korrek tot die naaste cm |
2.
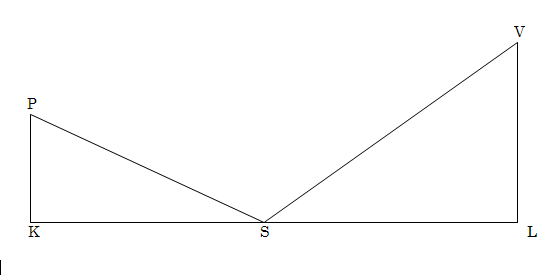
In die skets is PK die ooghoogte van die persoon, S is die posisie van die spieël en VL is die voorwerp waarvan die hoogte gemeet word. Verduidelik hoekom ΔPKS ΔVLS is.
3. In hierdie taak kan die afmetings onakkuraat wees. Verduidelik watter foute gemaak kan word wat die akkuraatheid van die bepaling van die hoogte van die voorwerp kan beïnvloed.
| LU 3 |
| Ruimte en Vorm (Meetkunde)Die leerder is in staat om eienskappe van en verwantskappe tussen tweedimensionele vorms en driedimensionele voorwerpe in ‘n verskeidenheid oriëntasies en posisies te beskryf en voor te stel. |
| Ons weet dit as die leerder: |
| 3.1 meetkundige figure en driedimensionele voorwerpe in natuurlike en kulturele vorms en meetkundige agtergrond herken, visualiseer en benoem, insluitend: |
| 3.1.1 reëlmatige en onreëlmatige veelhoeke en veelvlakke; |
| 3.1.2 sfere; |
| 3.1.3 silinders; |
| 3.2 die onderlinge verwantskappe van meetkundige figure en driedimensionele voorwerpe se eienskappe met bewyse in kontekste, insluitend dié wat gebruik kan word om ‘n bewustheid van sosiale, kulturele en omgewingsake te bevorder beskryf, insluitend:3.2.1 kongruensie en reguitlynmeetkunde; |
| 3.3 die meetkunde van reguitlyne en driehoeke gebruik om probleme op te los en verwantskappe in meetkundige figure te bewys; |
| 3.4 meetkundige figure teken en/of konstrueer en modelle maak van driedimensionele voorwerpe om die eienskappe daarvan en van modelsituasies in die omgewing te ondersoek en vergelyk; |
| 3.5 transformasies, kongruensie en gelykvormigheid gebruik om die eienskappe van meetkundige figure en driedimensionele voorwerpe te ondersoek (alleen en/of as ‘n lid van ‘n span of groep), insluitend toetse vir die gelykvormigheid en kongruensie van driehoeke. |

Notification Switch
Would you like to follow the 'Wiskunde graad 9' conversation and receive update notifications?