3.11 Signal sampling  (Page 2/3)

The sampling theorem

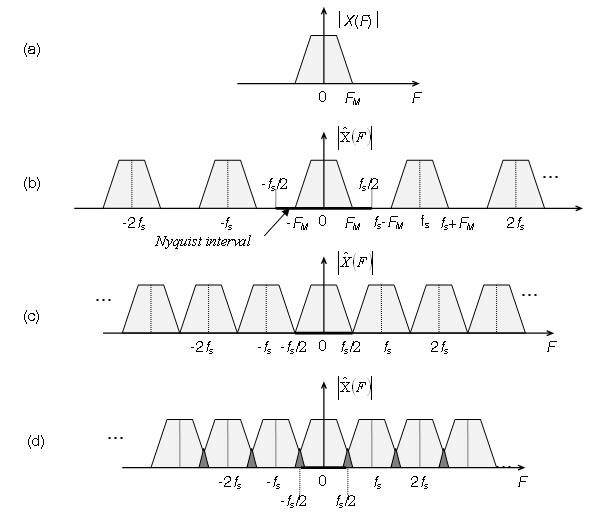
Let’s consider a certain continuous-time signal x(t) rpresenting certain information such as voice. Its magnitude frequency spectrum is assumed to be as in [link] a where FM is its maximum frequency.

The signal is sampled by a sequence of narrow pulses $\delta t$ of amplitude 1 as before. The Fourier series expansion (see section ) of this sampling function is

Hence the samples are

Where $\widehat{x}(t)$ denotes the samples, its Fourier frequency spectrum is $\widehat{X}(F)$ . Thus the spectrum of the sampled signal consists of that of the analog signal (with a multiplying factor $\delta t/T$ ) and its shifted versions to $\pm 2f_s,\pm 3f_s\mathrm{...}$ This spectrum can also obtain using the Fourier transform (see section ) instead of the Fourier series.

In [link] b the spectrum bands do not overlap so we can recover the analog signal by lowpass filtering the central band, or bandpass filtering any other bands. All the bands contain the same information but at different frequencies . In [link] c we still can recover the signal but with a precise filter. In [link] d the bands overlap and we are in no way to recover the analog signal. So the limiting case is [link] c. From this observation, the sampling theoren states as follows.

In order the samples represent correctly the analog signal, the sampling frequency must be greater than twice the maximum frequency of the analog signal:

The limiting frequency 2 $F_M$ is called Nyquist rate , and the central frequency interval (- $f_s$ /2, $f_s$ /2) is called the Nyquist interval .

For example if a waveform contains the fundamental frequency of 1 kHz and a second harmonic 2 kHz, then the sampling rate must be greater than 2 x 2 kHz = 4 kHz, say 5 kHz or more. Another example is for the voice in the telephone system. The voice is limited by a high quality analog filter at $F_M$ = 3.4 kHz, then the sampling frequency must be greater than 2 x 3.4 = 6.8 kHz, say 8 kHz or more.

In the case of [link] d there is a phenomenon called aliasing that will be discussed next.

Aliasing

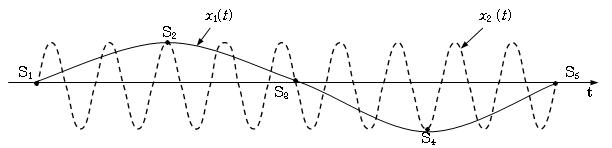
We would like to know what happens when the signal is sampled below the Nyquist rate, i.e. the sampling theorem is not satisfied. Look at [link] . The low-frequency signal $x_1(t)$ is sampled 4 times at $S_1,S_2,S_3$ and $S_4$ in a period of the signal, i.e $f_s=4F_{x1}$ . From these samples we would be able to recover $x_1(t)$ . For the high-frequency signal $x_2(t)$ there are the same 4 samples $S_1,S_2,S_3$ and $S_4$ in its 9 cycles, so the sampling frequency is just (4/9) $F_{\mathrm{x2}}$ i.e. under the Nyquist rate. From these sample points of $x_2(t)$ we will recover $x_1(t)$ and not the correct $x_2(t)$ . Thus the high frequency signal when undersampled will be recovered as a low-frequency signal. This phenomenon is called aliasing , and the recovered low frequency, which is false, is called the alias of the original high-frequency signal.