Legendrian knots and links

Remark 3.4 The converse to Theorem 3.3 is false: there exist non-Legendrian isotopic Legendrian knots whose Lagrangian projections are related by a finite sequence of the moves $\sigma \left(1\right)$ and $\sigma \left(2\right)$ .

Invariants of legendrian knots

Definition 4.1 The rotation number of an oriented Legendrian knot is

where $D$ is the number of down cusps in the front projection and $U$ is the number of up cusps.

Definition 4.2 The Thurston-Bennequin invariant , $tb\left(L\right)$ , is the linking number between $L$ and $L^{\text{'}}$ , where $L^{\text{'}}$ is a slight push-off of $L$ in the $z$ -direction.

That is, $tb\left(L\right)$ is one-half the signed count of the intersections between $L$ and $L^{\text{'}}$ , where we assign $\pm 1$ to intersections as in the following diagram:

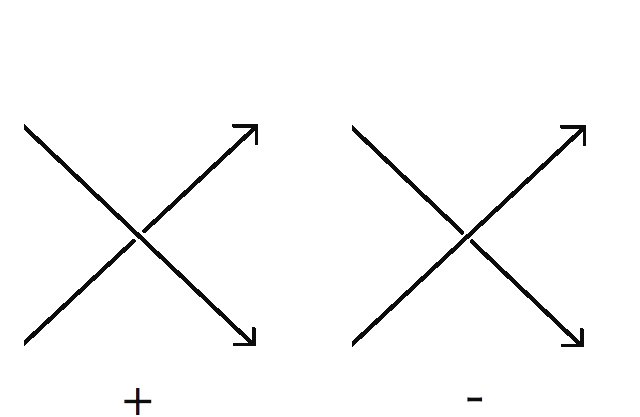
Theorem 4.3 Two oriented Legendrian torus knots are Legendrian isotopic if and only if their Thurston-Bennequin invariants, rotation numbers, and (topological) knot types agree.

Remark 4.4 Theorem 4.3 is not true for all knots. Y. Chekanov and Y. Eliashberg independently gave examples of non-Legendrian isotopic Legendrian knots with the same Thurston-Bennequin invariant, rotation number, and topological knot type.

Stick number

Definition 5.1 A stick knot is the image of a PL-embedding of $S^1$ in ${\mathbb{R}}^3$ . That is, a knot composed of line segments attached to each other at their endpoints. We call the segments edges and the joined endpoints vertices , and we require that exactly two edges meet at each vertex. The stick number $S\left(L\right)$ of a knot $L$ is the minimum number of sticks necessary to make $L$ in ${\mathbb{R}}^3$ .

Definition 5.2 A Legendrian stick knot is a stick knot that is Legendrian everywhere except at its vertices. The Legendrian stick number of a Legendrian knot $L$ , denoted $LS\left(L\right)$ , is the minimum number of sticks necessary to make a stick knot that is Legendrian isotopic to $L$ away from its vertices. The front stick number of $L$ , $FS\left(L\right)$ , is the minimum number of sticks in a front diagram of $L$ .

Remark 5.3 It is not hard to see that $LS\left(L\right)=2FS\left(L\right)$ . For, if a stick lies in $\xi$ then it is parametrized by a line segment

for $t\in I$ such that $y\left(t\right)x^{\text{'}}\left(t\right)-z^{\text{'}}\left(t\right)=0$ . In particular, either $m_x=m_z=0$ , in which case the stick runs perpendicular to the $xz$ -plane, or $m_y=0$ , and the stick lies in a plane parallel to the $xz$ -plane.

Example 5.4 $\phantom{M}$

1. a. The minimum $FS$ number over all Legendrian unknots is 3.
2. b. The Legendrian right-handed trefoil $T_R$ with $tb=1$ has $FS\left(T_R\right)=6$ . The (topological) right-handed trefoil has $S\left(T_R\right)=6$ .

Questions

1. Define isotopy for Legendrian stick knots.
2. Define Reidemeister moves for Legendrian stick knots in the front projection. Is there an analogue of Theorem 3.2?
3. Are there analogues of the Thurston-Bennequin invariant and rotation number for Legendrian stick knots? How do they behave under the Reidemeister moves?
4. Is there some relationship between $FS\left(L\right)$ and $S\left(L\right)$ ?
5. In an REU with J. Sabloff, J. Ralston and S. Sacchetti showed that for the maximal Thurston-Bennequin representative of the torus knot $T(2,2_{n-1})$ , $FS\left(T,(,2,,,2_{n-1},)\right)\le 2n+4$ . Can this be improved? Is there a bound for general torus knots?

Acknowledgments

This Connexions module describes work conducted as part of Rice University's VIGRE program, supported by National Science Foundation grant DMS-0739420. We would like to thank Dr. Josh Sabloff for suggesting this problem on Legendrian sticks, Dr. Shelly Harvey for assisting in the organization of our PFUG, and the undergraduate members C. Buenger, A. Jamshidi, S. Kruzick, A. Mehta, and M. Scherf.