0.5 Cơ cấu điện từ  (Page 2/4)

Tính từ dẫn khe hở không khí của mạch từ

Tính từ dẫn bằng phương pháp phân chia từ trường

Xét ví dụ : Có một cực từ tiết diện chữ nhật đặt song song với mặt phẳng. Giả thiết chiều  đi từ cực từ xuống mặt phẳng (hình minh họa).

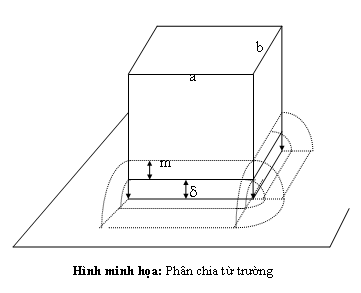
Nếu tính từ dẫn khe hở bằng phương pháp phân chia từ trường ta sẽ phân từ trường thành nhiều phần nhỏ sao cho ở mỗi phần từ trường phân bố đều(có các đường sức từ song song với nhau) để áp dụng công thức cơ bản tính từ dẫn đã có ở trên. Ở đây ta chia làm 17 phần gồm :

+) 1 hình hộp chữ nhật thể tích: a. b. 

+) 4 hình 1/4 trụ tròn có đường kính 2 chiều cao a và b

+) 4 hình trụ 1/4 rỗng có đường kính trong 2 đường kính ngoài 2 + 2m

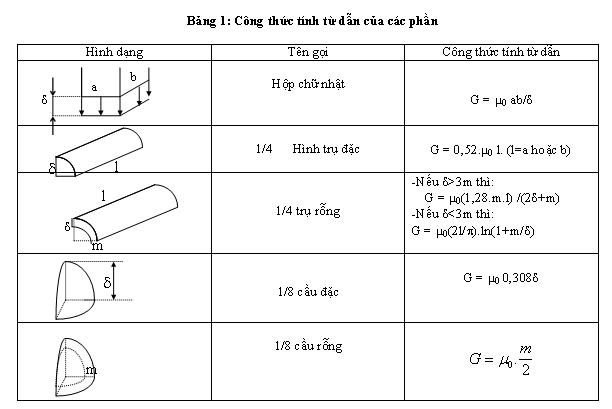
Từ dẫn của từng phần cho theo bảng 1. Trong đó từ dẫn chính G là của trụ chữ nhật, tổng các từ dẫn còn lại là từ dẫn tản. Có $G=\sum _{i=1}^{\text{17}}{G}_i$ : nếu có hai từ dẫn nối song song thì nối từ dẫn tương đương Gtđ= G1 + G2.

Nếu nối tiếp thì từ dẫn tương đương là $G_{\mathrm{tâ}}=\frac{G_1{G}_2}{G_1+G_2}$ .

Ưu điểm : tính bằng phương pháp này có ưu điểm là chính xác, rõ ràng dễ kiểm tra.

Nhược điểm : có nhiều công thức nên chỉ dùng để tính kiểm nghiệm

Tính từ dẫn bằng công thức kinh nghiệm ( dùng khi tính toán sơ bộ )

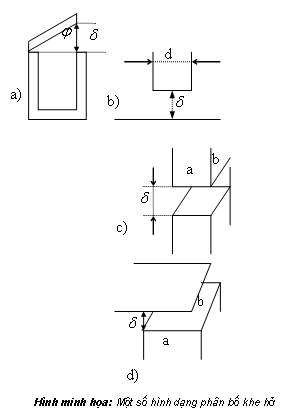
A) từ dẫn khe hở không khí giữa nắp và lõi tạo thành góc  (hình a)

G = K . G0

Với: K: hệ số điều chỉnh

$$ $K=\mathrm{2,}\text{75}\sqrt[4]{\varphi }$ , ( tính theo rađian).

$\begin{array}{}\\ \\ \end{array}$ + $G_0={\mu }_0\text{.}\frac{S}{\delta }$

+ S :tiết diện lõi [cm2].

+  : độ dài trung bình khe hở không khí (cm).

0 = 1,25 . 10-8 [ wb/a. cm= h/cm].

B ) từ dẫn giữa cực từ tròn với mặt phẳng (hình b)

$G_0={\mu }_0\text{.}\frac{S}{\delta }1+\frac{\mathrm{2,}\text{08}}{d}\delta $

C) từ dẫn giữa hai cực từ chữ nhật(hình c)

$G=K\text{.}{\mu }_0\text{.}\frac{S}{\delta }=K\text{.}{G}_0$

$K=1+\frac{\mathrm{0,}\text{58}}{m\text{.}n}1+m+\frac{\mathrm{0,}\text{31}}{m\text{.}{n}^2}$ , với $m=\frac{b}{a};n=\frac{a}{\delta }$

D) từ dẫn giữa mặt phẳng và cực từ đặt ở đầu mặt phẳng(hình d)

G = k .g0 = k .0 . s/

Với k=1+0,58m.n1+1,5m+0,31m.n2 size 12{k=1+ { {0,"58"} over {m "." n} } left (1+1,5m right )+ { {0,"31"} over {m "." n rsup { size 8{2} } } } } {}

e) Từ dẫn giữa mặt phẳng và cực từ đặt ở giữa mặt phẳng

$G=K\text{.}{\mu }_0\text{.}\frac{S}{\delta }=K\text{.}{G}_0$

$K=1+\frac{\mathrm{0,}\text{58}}{m\text{.}n}1+\mathrm{2m}+\frac{\mathrm{0,}\text{31}}{m\text{.}{n}^2}$

Tính từ dẫn bằng phương pháp giải tích

Nguyên tắc của phương pháp này là dựa vào tính chất tương đương giữa sự phân bố từ trường xung quanh vật dẫn từ với điện trường xung quanh vật dẫn điện. Điều kiện bờ giống nhau thì cũng giải tương tự.

Ví dụ: hai vật dẫn từ đặt song song với nhau, nếu ở điện trường thì có công thức:

$\begin{array}{}\text{Q=C}({\varphi }_1-{\varphi }_2)\\ Q\text{laì}\text{âiãûn têch trãn váût dáùn}\text{.}\\ C\text{laì}\text{âiãûn dung}\text{.}\\ {\varphi }_1,{\varphi }_2\text{laì}\text{âiãûn thãú cuía váût dáùn 1 vaì 2}\text{.}\end{array}$

Với điện tích Q, điện dung C, điện thế .

Ỏ̉ từ trường có : $\phi =Gu_1-u_2$ với:

$\begin{array}{}\phi \text{laì tæì thäng giæîa hai váût dáùn}\text{.}\\ \text{G laì tæì dáùn giæîa hai váût dáùn}\text{.}\\ U_1,U_2:\text{laì tæì thãú cuía váût dáùn 1 vaì 2}\text{.}\end{array}$

có: $G=K\text{.}C$ và K: hệ số phụ thuộc đơn vị chọn.

Ở đây: $K=\frac{{\mu }_0}{{\epsilon }_0}$ với ${\mu }_0=\mathrm{1,}\text{25}\text{.}{\text{10}}^{-8}\frac{W\text{.}b}{\text{Acm}};{\epsilon }_0=\frac{1}{\mathrm{4\pi }\text{.}9\text{.}{\text{10}}^{\text{11}}}[F/\text{cm}]$

Vậy với mô hình toán học giống nhau khi đã tìm ra điện dung C thì sẽ tìm ra từ dẫn G.