0.9 Appendix c  (Page 3/3)

Relationship between the basic tdm-fdm and fdm-tdm transmultiplexers

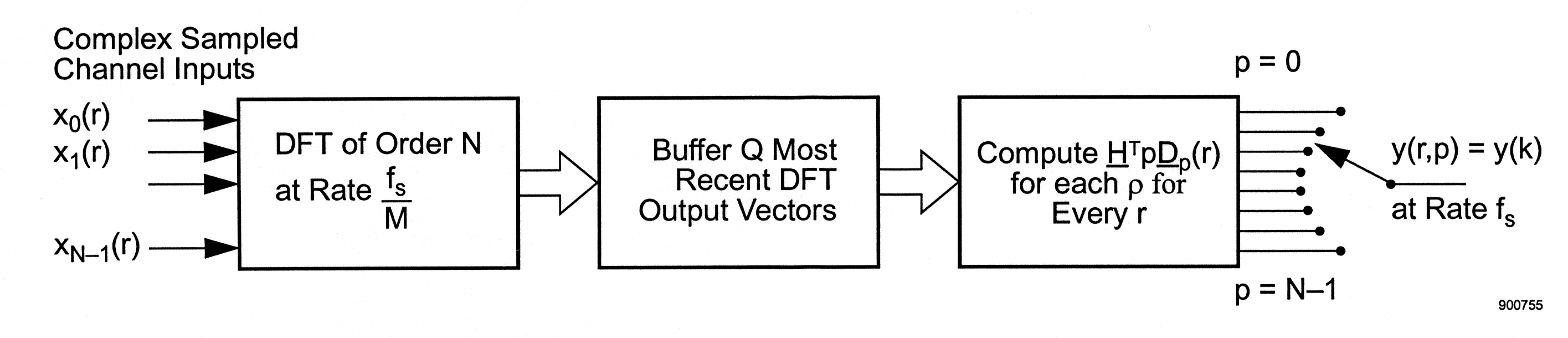
We immediately observe that this computation is exactly that required to demultiplex all N channels in a basic FDM-to-TDM transmux. In fact, the FDM-TDM and TDM-FDM transmultiplexers are mathematical duals of each other and virtually any manipulation feasible with one has its analog in the other. They are not precisely the same, however. An example is the definition of Q and $\overline{Q}$ . The former depends on f _s and N , the number of channels, while the latter depends on f _s and M , the interpolation factor. For the basic transmux equations $N=M$ and the two are identical, but the fundamental relationship is duality, not equality.

Practically, however, many things are the same. The computation rate has already been shown to be the same (when the pulse response durations are the same) and the block diagrams are reversed forms of each other. A few other practical observations can be made:

• Picking M is tantamount to choosing f _s .
• Making $M=N$ is equivalent to making the channel tuning frequencies equal to the centers of the images created by the zero-filling.
• The pulse response $h\left(\ell \right)$ controls how much of $x_n\left(r\right)$ leaks into other FDM channels. The design of $h\left(\ell \right)$ is a compromise between the degree of acceptable passband amplitude distortion, the degree to which the images of the input signal must be suppressed, and the filter order L , which proportionally influences the computation needed for the transmultiplexer.

A pair of examples

What is an FDM-TDM Transmultiplexer describes several general uses for the FDM-TDM transmultiplexer and The Impact of Digital Tuning on the Overall design of an FDM-TDM Transmux examined several case histories of such transmultiplexers when used to solve practical problems. Such depth is not appropriate here, but it useful to see ways in which the TDM-FDM transmultiplexer is used.

[link] (a) shows a commercial telephone switching application. Several FDM signals enter the system and are demultiplexed by using FDM-TDM transmultiplexers. The demultiplexed channels are presented in a TDM form to the digital switch that reorganizes the voice channel samples in the TDM stream based on the customer's dialled number. The output TDM data is then converted back to FDM form by using TDM-to-FDM transmultiplexers. While it may seem curious to convert to TDM form to perform the switching, it is commonly done owing to the low cost of digital switching, the high cost of direct switching (for example, translating) of FDM channels, and the large number of existing analog transmission systems [circa the 1980s].

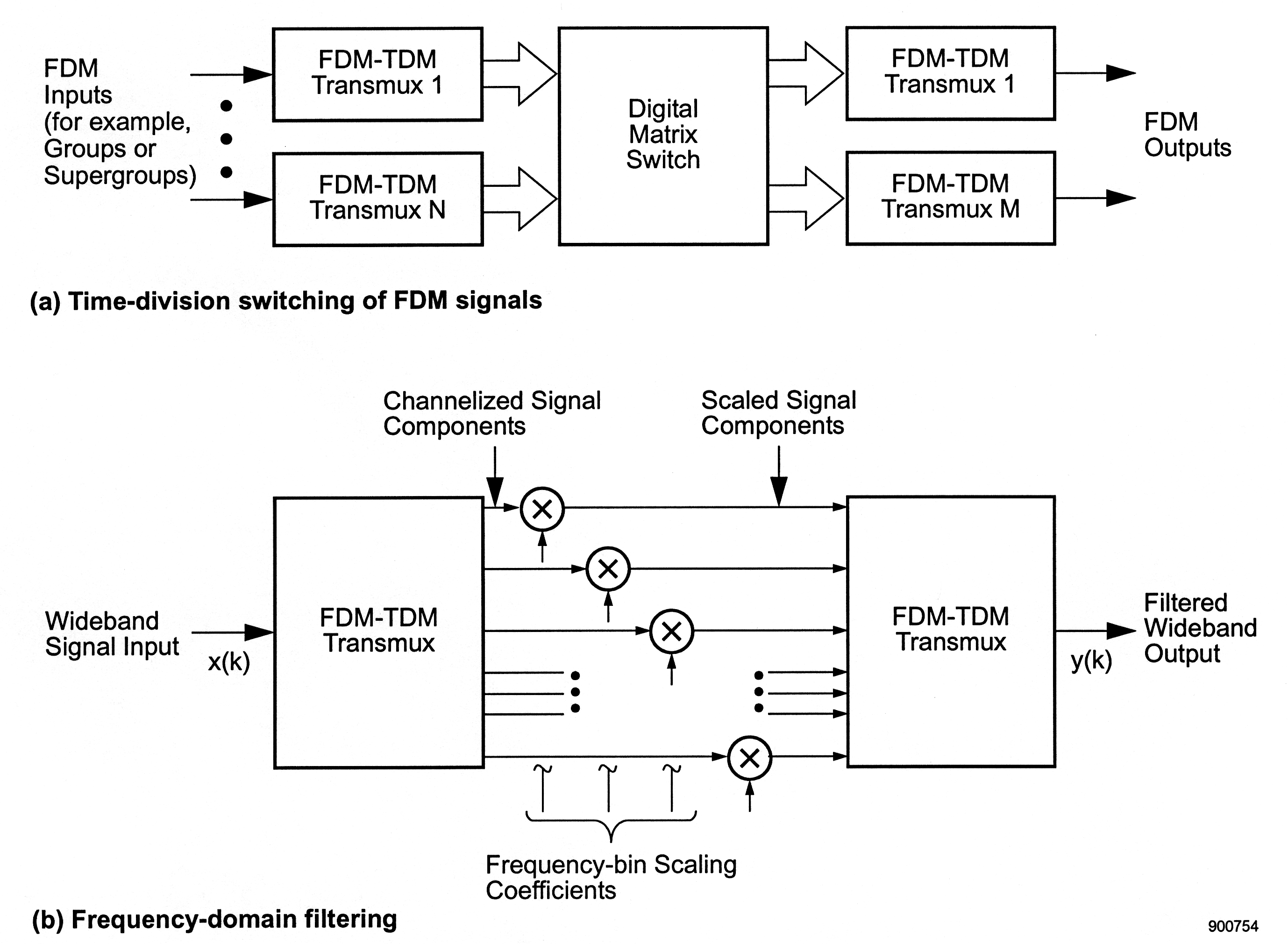
[link] (b) shows another example of a TDM-to-FDM transmultiplexer, this one also paired with a FDM-TDM transmultiplexer. The objective of this architecture is to form an easily controlled, high-resolution digital FIR filter. The input signal is decomposed into N unique bins centered at multiples of $\frac{f_s}{N}$ Hz, where f _s is the input sampling rate. The output of each bin is scaled by its own gain w _n and then applied to a TDM-FDM transmultiplexer, whose output is the filter output. If the weighting functions for the two transmultiplexers, $h_f\left(\ell \right)$ and $h_t\left(\ell \right)$ , respectively, are chosen so that each equivalent tuner has bandwidth of about $\frac{f_s}{N}$ , then it can be seen that this structure resembles a graphic equalizer of the type used in stereo equipment. If all gains $\left\{w_n\right\}$ are equal to unity, then the input signal is decomposed and then recomposed without significant change. If energy at a specific frequency needs to be removed from the output, then all weights except the one corresponding to the bin with the offending energy are set to unity while that one is lowered, potentially to zero. The concept carries forward to the design of filters with rather general amplitude and phase responses with the proper choice of the weights. The pulse response of the structure has duration of about $L_f+L_t=(Q_f+Q_t)N$ , depending on how h _f and h _t are selected, and the filter has N degrees of freedom.

Why is this filter structure attractive if it offers the user fewer degrees of freedom in pulse response selection than the effective length of the filter pulse response? The answer comes in its ease of control. A single change in a single coefficient of a conventional transversal FIR filter changes the frequency response of the filter at all frequencies. Conversely, with the transmultiplexer/channel bank approach, the change of one coefficient affects only a spectral band known a priori to the user.

This type of behavior makes it well suited to use in adaptive digital filters, and particularly in those whose purpose is to remove concentrated interfering signals from the signal of actual interest to the user. An FDM-TDM/TDM-FDM transmultiplexer pair used to build such an adaptive filter is described in [link] .