| << Chapter < Page | Chapter >> Page > |
Find the equation of the line tangent to the graph of at
We can use [link] , but as we have seen, the results are the same if we use [link] .
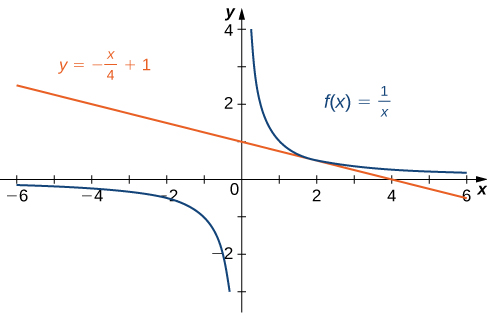
We now know that the slope of the tangent line is To find the equation of the tangent line, we also need a point on the line. We know that Since the tangent line passes through the point we can use the point-slope equation of a line to find the equation of the tangent line. Thus the tangent line has the equation The graphs of and are shown in [link] .
The type of limit we compute in order to find the slope of the line tangent to a function at a point occurs in many applications across many disciplines. These applications include velocity and acceleration in physics, marginal profit functions in business, and growth rates in biology. This limit occurs so frequently that we give this value a special name: the derivative . The process of finding a derivative is called differentiation .
Let be a function defined in an open interval containing The derivative of the function at denoted by is defined by
provided this limit exists.
Alternatively, we may also define the derivative of at as
For use a table to estimate using [link] .
Create a table using values of just below and just above
After examining the table, we see that a good estimate is
For find by using [link] .
Substitute the given function and value directly into the equation.
For find by using [link] .
Using this equation, we can substitute two values of the function into the equation, and we should get the same value as in [link] .
Now that we can evaluate a derivative, we can use it in velocity applications. Recall that if is the position of an object moving along a coordinate axis, the average velocity of the object over a time interval if or if is given by the difference quotient

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?