| << Chapter < Page | Chapter >> Page > |
To answer this question, let’s look at [link] again. The local extrema occur at and Notice that at and the derivative At the derivative does not exist, since the function has a corner there. In fact, if has a local extremum at a point the derivative must satisfy one of the following conditions: either or is undefined. Such a value is known as a critical point and it is important in finding extreme values for functions.
Let be an interior point in the domain of We say that is a critical point of if or is undefined.
As mentioned earlier, if has a local extremum at a point then must be a critical point of This fact is known as Fermat’s theorem .
If has a local extremum at and is differentiable at then
Suppose has a local extremum at and is differentiable at We need to show that To do this, we will show that and and therefore Since has a local extremum at has a local maximum or local minimum at Suppose has a local maximum at The case in which has a local minimum at can be handled similarly. There then exists an open interval such that for all Since is differentiable at from the definition of the derivative, we know that
Since this limit exists, both one-sided limits also exist and equal Therefore,
and
Since is a local maximum, we see that for near Therefore, for near but we have From [link] we conclude that Similarly, it can be shown that Therefore,
□
From Fermat’s theorem, we conclude that if has a local extremum at then either or is undefined. In other words, local extrema can only occur at critical points.
Note this theorem does not claim that a function must have a local extremum at a critical point. Rather, it states that critical points are candidates for local extrema. For example, consider the function We have when Therefore, is a critical point. However, is increasing over and thus does not have a local extremum at In [link] , we see several different possibilities for critical points. In some of these cases, the functions have local extrema at critical points, whereas in other cases the functions do not. Note that these graphs do not show all possibilities for the behavior of a function at a critical point.
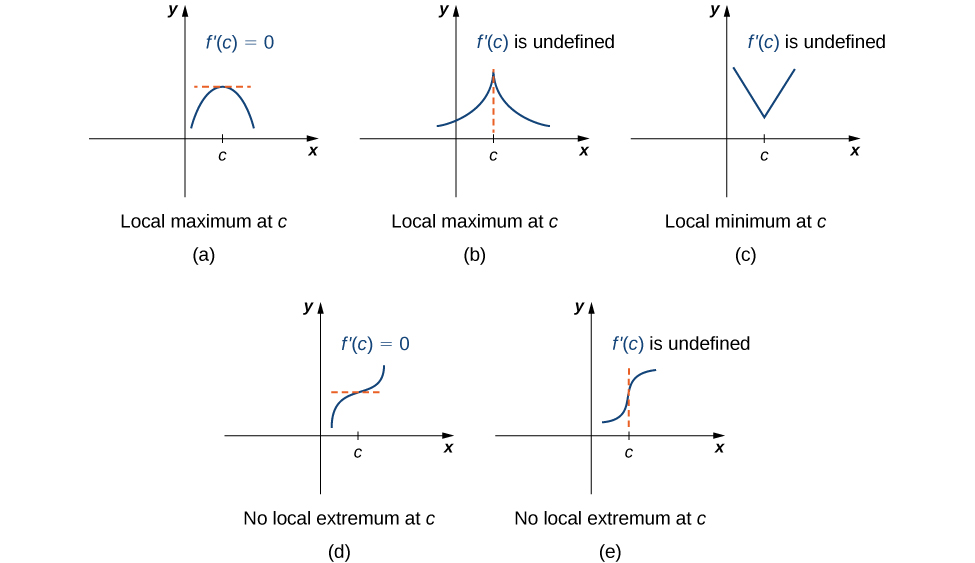
Later in this chapter we look at analytical methods for determining whether a function actually has a local extremum at a critical point. For now, let’s turn our attention to finding critical points. We will use graphical observations to determine whether a critical point is associated with a local extremum.
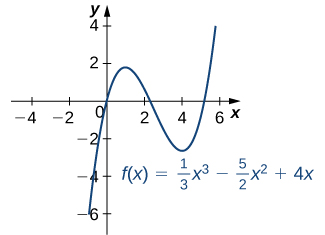
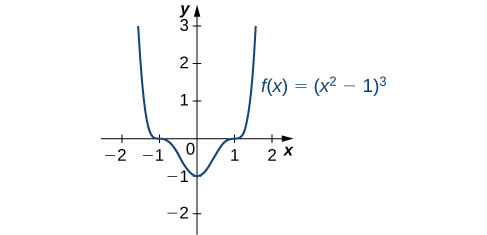
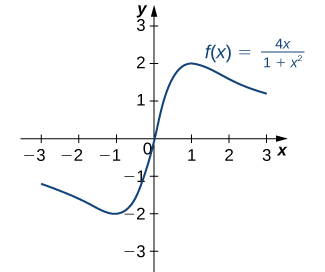
For each of the following functions, find all critical points. Use a graphing utility to determine whether the function has a local extremum at each of the critical points.

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?