| << Chapter < Page | Chapter >> Page > |
Select the best method to find the volume of a solid of revolution generated by revolving the given region around the and set up the integral to find the volume (do not evaluate the integral): the region bounded by the graphs of and
Use the method of washers;
For the following exercise, find the volume generated when the region between the two curves is rotated around the given axis. Use both the shell method and the washer method. Use technology to graph the functions and draw a typical slice by hand.
[T] Over the curve of and rotated around the
[T] Over the curve of rotated around the
[T] Under the curve of rotated around the
For the following exercises, use shells to find the volumes of the given solids. Note that the rotated regions lie between the curve and the and are rotated around the
For the following exercises, use shells to find the volume generated by rotating the regions between the given curve and around the
For the following exercises, find the volume generated when the region between the curves is rotated around the given axis.
rotated around the
rotated around the
rotated around the line
rotated around the line
rotated around the line
For the following exercises, use technology to graph the region. Determine which method you think would be easiest to use to calculate the volume generated when the function is rotated around the specified axis. Then, use your chosen method to find the volume.
[T] and rotated around the
[T] rotated around the
[T] rotated around the
[T] and rotated around the
For the following exercises, use the method of shells to approximate the volumes of some common objects, which are pictured in accompanying figures.
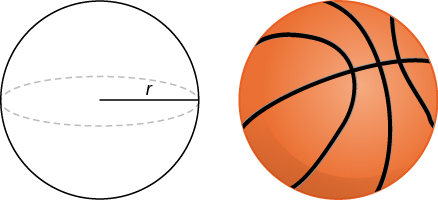
Use the method of shells to find the volume of a sphere of radius
Use the method of shells to find the volume of a cone with radius and height
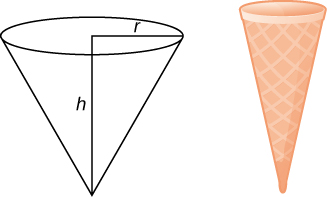
units 3
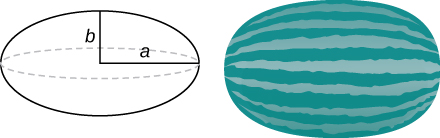
Use the method of shells to find the volume of an ellipse rotated around the
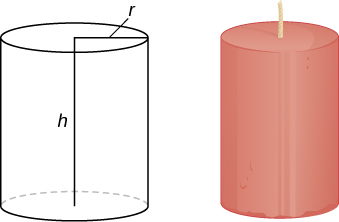
Use the method of shells to find the volume of a cylinder with radius and height
units 3
Use the method of shells to find the volume of the donut created when the circle is rotated around the line
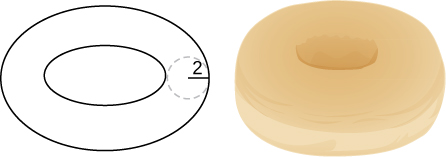
Consider the region enclosed by the graphs of and What is the volume of the solid generated when this region is rotated around the Assume that the function is defined over the interval
units 3
Consider the function which decreases from to Set up the integrals for determining the volume, using both the shell method and the disk method, of the solid generated when this region, with and is rotated around the Prove that both methods approximate the same volume. Which method is easier to apply? ( Hint: Since is one-to-one, there exists an inverse

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?