4.9 Newton’s method

In many areas of pure and applied mathematics, we are interested in finding solutions to an equation of the form $f\left(x\right)=0.$ For most functions, however, it is difficult—if not impossible—to calculate their zeroes explicitly. In this section, we take a look at a technique that provides a very efficient way of approximating the zeroes of functions . This technique makes use of tangent line approximations and is behind the method used often by calculators and computers to find zeroes.

Describing newton’s method

Consider the task of finding the solutions of $f\left(x\right)=0.$ If $f$ is the first-degree polynomial $f\left(x\right)=ax+b,$ then the solution of $f\left(x\right)=0$ is given by the formula $x=-\frac{b}{a}.$ If $f$ is the second-degree polynomial $f\left(x\right)=a{x}^2+bx+c,$ the solutions of $f\left(x\right)=0$ can be found by using the quadratic formula. However, for polynomials of degree $3$ or more, finding roots of $f$ becomes more complicated. Although formulas exist for third- and fourth-degree polynomials, they are quite complicated. Also, if $f$ is a polynomial of degree $5$ or greater, it is known that no such formulas exist. For example, consider the function

No formula exists that allows us to find the solutions of $f\left(x\right)=0.$ Similar difficulties exist for nonpolynomial functions. For example, consider the task of finding solutions of $\text{tan}\left(x\right)-x=0.$ No simple formula exists for the solutions of this equation. In cases such as these, we can use Newton’s method to approximate the roots.

Newton’s method    makes use of the following idea to approximate the solutions of $f\left(x\right)=0.$ By sketching a graph of $f,$ we can estimate a root of $f\left(x\right)=0.$ Let’s call this estimate $x_0.$ We then draw the tangent line to $f$ at $x_0.$ If $f^{\prime }\left(x_0\right)\ne 0,$ this tangent line intersects the $x$ -axis at some point $\left(x_1,0\right).$ Now let $x_1$ be the next approximation to the actual root. Typically, $x_1$ is closer than $x_0$ to an actual root. Next we draw the tangent line to $f$ at $x_1.$ If $f^{\prime }\left(x_1\right)\ne 0,$ this tangent line also intersects the $x$ -axis, producing another approximation, $x_2.$ We continue in this way, deriving a list of approximations: $x_0,x_1,x_2\text{,…}.$ Typically, the numbers $x_0,x_1,x_2\text{,…}$ quickly approach an actual root $x*,$ as shown in the following figure.

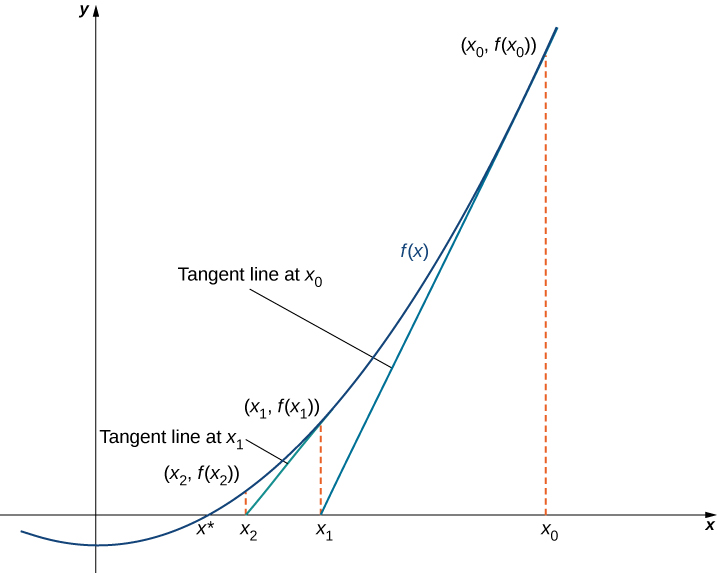
Now let’s look at how to calculate the approximations $x_0,x_1,x_2\text{,…}.$ If $x_0$ is our first approximation, the approximation $x_1$ is defined by letting $\left(x_1,0\right)$ be the $x$ -intercept of the tangent line to $f$ at $x_0.$ The equation of this tangent line is given by

Therefore, $x_1$ must satisfy

Solving this equation for $x_1,$ we conclude that

Similarly, the point $\left(x_2,0\right)$ is the $x$ -intercept of the tangent line to $f$ at $x_1.$ Therefore, $x_2$ satisfies the equation

In general, for $n>0,x_n$ satisfies

Next we see how to make use of this technique to approximate the root of the polynomial $f\left(x\right)=x^3-3x+1.$