| << Chapter < Page | Chapter >> Page > |
The following table gives approximate values of the average annual atmospheric rate of increase in carbon dioxide (CO 2 ) each decade since 1960, in parts per million (ppm). Estimate the total increase in atmospheric CO 2 between 1964 and 2013.
| Decade | Ppm/y |
|---|---|
| 1964–1973 | 1.07 |
| 1974–1983 | 1.34 |
| 1984–1993 | 1.40 |
| 1994–2003 | 1.87 |
| 2004–2013 | 2.07 |
The following table gives the approximate increase in sea level in inches over 20 years starting in the given year. Estimate the net change in mean sea level from 1870 to 2010.
| Starting Year | 20-Year Change |
|---|---|
| 1870 | 0.3 |
| 1890 | 1.5 |
| 1910 | 0.2 |
| 1930 | 2.8 |
| 1950 | 0.7 |
| 1970 | 1.1 |
| 1990 | 1.5 |
Add the numbers to get 8.1-in. net increase.
The following table gives the approximate increase in dollars in the average price of a gallon of gas per decade since 1950. If the average price of a gallon of gas in 2010 was $2.60, what was the average price of a gallon of gas in 1950?
| Starting Year | 10-Year Change |
|---|---|
| 1950 | 0.03 |
| 1960 | 0.05 |
| 1970 | 0.86 |
| 1980 | −0.03 |
| 1990 | 0.29 |
| 2000 | 1.12 |
The following table gives the percent growth of the U.S. population beginning in July of the year indicated. If the U.S. population was 281,421,906 in July 2000, estimate the U.S. population in July 2010.
| Year | % Change/Year |
|---|---|
| 2000 | 1.12 |
| 2001 | 0.99 |
| 2002 | 0.93 |
| 2003 | 0.86 |
| 2004 | 0.93 |
| 2005 | 0.93 |
| 2006 | 0.97 |
| 2007 | 0.96 |
| 2008 | 0.95 |
| 2009 | 0.88 |
( Hint: To obtain the population in July 2001, multiply the population in July 2000 by 1.0112 to get 284,573,831.)
309,389,957
In the following exercises, estimate the areas under the curves by computing the left Riemann sums, L 8 .
[T] Use a computer algebra system to compute the Riemann sum, for for on
[T] Use a computer algebra system to compute the Riemann sum, L N , for for on
[T] Use a computer algebra system to compute the Riemann sum, L N , for for on Compare these estimates with π .
In the following exercises, use a calculator or a computer program to evaluate the endpoint sums R N and L N for How do these estimates compare with the exact answers, which you can find via geometry?
[T] on the interval
and By symmetry of the graph, the exact area is zero.
[T] on the interval
In the following exercises, use a calculator or a computer program to evaluate the endpoint sums R N and L N for
[T] on the interval which has an exact area of
Explain why, if and f is increasing on that the left endpoint estimate is a lower bound for the area below the graph of f on
If is a subinterval of under one of the left-endpoint sum rectangles, then the area of the rectangle contributing to the left-endpoint estimate is But, for so the area under the graph of f between c and d is plus the area below the graph of f but above the horizontal line segment at height which is positive. As this is true for each left-endpoint sum interval, it follows that the left Riemann sum is less than or equal to the area below the graph of f on
Explain why, if and f is decreasing on that the left endpoint estimate is an upper bound for the area below the graph of f on
Show that, in general,
and The left sum has a term corresponding to and the right sum has a term corresponding to In any term corresponding to occurs once with a plus sign and once with a minus sign, so each such term cancels and one is left with
Explain why, if f is increasing on the error between either L N or R N and the area A below the graph of f is at most
For each of the three graphs:
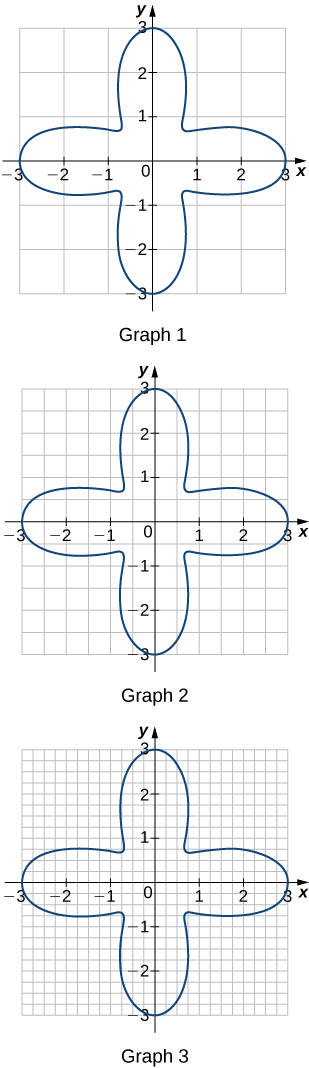
Graph 1: a. b. Graph 2: a. b. Graph 3: a. b.
In the previous exercise, explain why gets no smaller while gets no larger as the squares are subdivided into four boxes of equal area.
A unit circle is made up of n wedges equivalent to the inner wedge in the figure. The base of the inner triangle is 1 unit and its height is The base of the outer triangle is and the height is Use this information to argue that the area of a unit circle is equal to π .
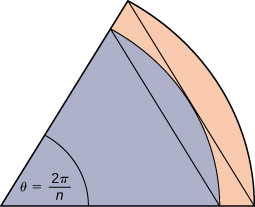
Let A be the area of the unit circle. The circle encloses n congruent triangles each of area so Similarly, the circle is contained inside n congruent triangles each of area so As so we conclude Also, as so we also have By the squeeze theorem for limits, we conclude that

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?