4.5 Derivatives and the shape of a graph

Earlier in this chapter we stated that if a function $f$ has a local extremum at a point $c,$ then $c$ must be a critical point of $f.$ However, a function is not guaranteed to have a local extremum at a critical point. For example, $f(x)=x^3$ has a critical point at $x=0$ since $f\prime (x)=3x^2$ is zero at $x=0,$ but $f$ does not have a local extremum at $x=0.$ Using the results from the previous section, we are now able to determine whether a critical point of a function actually corresponds to a local extreme value. In this section, we also see how the second derivative provides information about the shape of a graph by describing whether the graph of a function curves upward or curves downward.

The first derivative test

Corollary $3$ of the Mean Value Theorem showed that if the derivative of a function is positive over an interval $I$ then the function is increasing over $I.$ On the other hand, if the derivative of the function is negative over an interval $I,$ then the function is decreasing over $I$ as shown in the following figure.

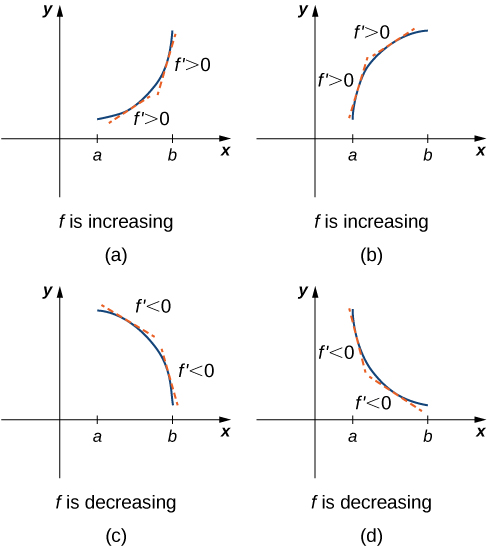
A continuous function $f$ has a local maximum at point $c$ if and only if $f$ switches from increasing to decreasing at point $c.$ Similarly, $f$ has a local minimum at $c$ if and only if $f$ switches from decreasing to increasing at $c.$ If $f$ is a continuous function over an interval $I$ containing $c$ and differentiable over $I,$ except possibly at $c,$ the only way $f$ can switch from increasing to decreasing (or vice versa) at point $c$ is if $f^{\prime }$ changes sign as $x$ increases through $c.$ If $f$ is differentiable at $c,$ the only way that $f^{\prime }.$ can change sign as $x$ increases through $c$ is if $f^{\prime }\left(c\right)=0.$ Therefore, for a function $f$ that is continuous over an interval $I$ containing $c$ and differentiable over $I,$ except possibly at $c,$ the only way $f$ can switch from increasing to decreasing (or vice versa) is if $f\prime \left(c\right)=0$ or $f^{\prime }\left(c\right)$ is undefined. Consequently, to locate local extrema for a function $f,$ we look for points $c$ in the domain of $f$ such that $f\prime \left(c\right)=0$ or $f^{\prime }\left(c\right)$ is undefined. Recall that such points are called critical points of $f.$

Note that $f$ need not have a local extrema at a critical point. The critical points are candidates for local extrema only. In [link] , we show that if a continuous function $f$ has a local extremum, it must occur at a critical point, but a function may not have a local extremum at a critical point. We show that if $f$ has a local extremum at a critical point, then the sign of $f^{\prime }$ switches as $x$ increases through that point.