| << Chapter < Page | Chapter >> Page > |
The electromagnetic wave model of light (as formulated by Maxwell) was one of the great triumphs of nineteenth-century science. In 1887, when Heinrich Hertz actually made invisible electromagnetic waves (what today are called radio waves) on one side of a room and detected them on the other side, it ushered in a new era that led to the modern age of telecommunications. His experiment ultimately led to the technologies of television, cell phones, and today’s wireless networks around the globe.
However, by the beginning of the twentieth century, more sophisticated experiments had revealed that light behaves in certain ways that cannot be explained by the wave model. Reluctantly, physicists had to accept that sometimes light behaves more like a “particle”—or at least a self-contained packet of energy—than a wave. We call such a packet of electromagnetic energy a photon .
The fact that light behaves like a wave in certain experiments and like a particle in others was a very surprising and unlikely idea. After all, our common sense says that waves and particles are opposite concepts. On one hand, a wave is a repeating disturbance that, by its very nature, is not in only one place, but spreads out. A particle, on the other hand, is something that can be in only one place at any given time. Strange as it sounds, though, countless experiments now confirm that electromagnetic radiation can sometimes behave like a wave and at other times like a particle.
Then, again, perhaps we shouldn’t be surprised that something that always travels at the “speed limit” of the universe and doesn’t need a medium to travel through might not obey our everyday common sense ideas. The confusion that this wave-particle duality of light caused in physics was eventually resolved by the introduction of a more complicated theory of waves and particles, now called quantum mechanics. (This is one of the most interesting fields of modern science, but it is mostly beyond the scope of our book. If you are interested in it, see some of the suggested resources at the end of this chapter.)
In any case, you should now be prepared when scientists (or the authors of this book) sometimes discuss electromagnetic radiation as if it consisted of waves and at other times refer to it as a stream of photons. A photon (being a packet of energy) carries a specific amount of energy. We can use the idea of energy to connect the photon and wave models. How much energy a photon has depends on its frequency when you think about it as a wave. A low-energy radio wave has a low frequency as a wave, while a high-energy X-ray at your dentist’s office is a high-frequency wave. Among the colors of visible light, violet-light photons have the highest energy and red-light photons have the lowest.
Test whether the connection between photons and waves is clear to you. In the above example, which photon would have the longer wavelength as a wave: the radio wave or the X-ray? If you answered the radio wave, you are correct. Radio waves have a lower frequency, so the wave cycles are longer (they are elephants, not miniature ponies).
Let’s think for a moment about how light from a lightbulb moves through space. As waves expand, they travel away from the bulb, not just toward your eyes but in all directions. They must therefore cover an ever-widening space. Yet the total amount of light available can’t change once the light has left the bulb. This means that, as the same expanding shell of light covers a larger and larger area, there must be less and less of it in any given place. Light (and all other electromagnetic radiation) gets weaker and weaker as it gets farther from its source.
The increase in the area that the light must cover is proportional to the square of the distance that the light has traveled ( [link] ). If we stand twice as far from the source, our eyes will intercept two-squared (2 × 2), or four times less light. If we stand 10 times farther from the source, we get 10-squared, or 100 times less light. You can see how this weakening means trouble for sources of light at astronomical distances. One of the nearest stars, Alpha Centauri A, emits about the same total energy as the Sun. But it is about 270,000 times farther away, and so it appears about 73 billion times fainter. No wonder the stars, which close-up would look more or less like the Sun, look like faint pinpoints of light from far away.
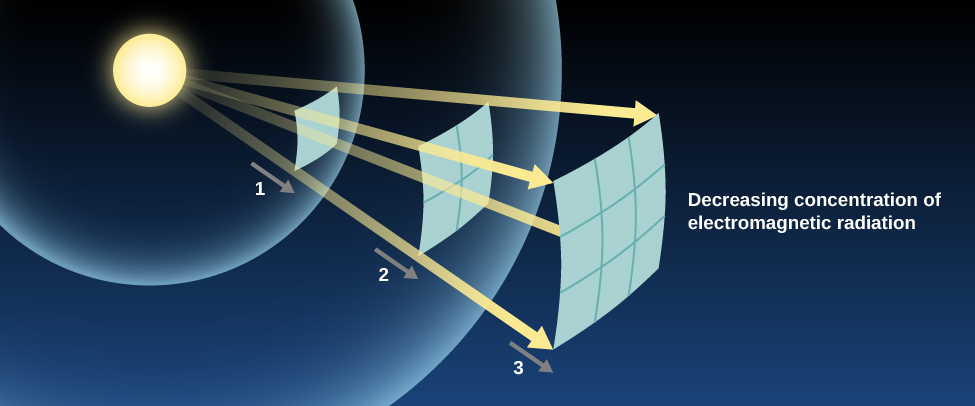
This idea—that the apparent brightness of a source (how bright it looks to us) gets weaker with distance in the way we have described—is known as the inverse square law for light propagation. In this respect, the propagation of light is similar to the effects of gravity. Remember that the force of gravity between two attracting masses is also inversely proportional to the square of their separation.
a. ; b. ; c.
James Clerk Maxwell showed that whenever charged particles change their motion, as they do in every atom and molecule, they give off waves of energy. Light is one form of this electromagnetic radiation. The wavelength of light determines the color of visible radiation. Wavelength (λ) is related to frequency ( f ) and the speed of light ( c ) by the equation c = λ f . Electromagnetic radiation sometimes behaves like waves, but at other times, it behaves as if it were a particle—a little packet of energy, called a photon. The apparent brightness of a source of electromagnetic energy decreases with increasing distance from that source in proportion to the square of the distance—a relationship known as the inverse square law.

Notification Switch
Would you like to follow the 'Astronomy' conversation and receive update notifications?