| << Chapter < Page | Chapter >> Page > |
Factor: .
The leading coefficient is negative, so the GCF will be negative.?
| Since the leading coefficient is negative, the GCF is negative, −6
a .
|
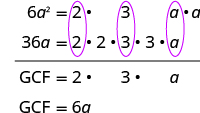
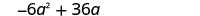
|
| Rewrite each term using the GCF. |
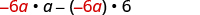 |
| Factor the GCF. |
 |
| Check. | |
Factor: .
The GCF is the binomial .
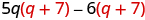 | |
| Factor the GCF, ( q + 7). |
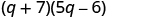 |
| Check on your own by multiplying. |
When there is no common factor of all the terms of a polynomial, look for a common factor in just some of the terms. When there are four terms, a good way to start is by separating the polynomial into two parts with two terms in each part. Then look for the GCF in each part. If the polynomial can be factored, you will find a common factor emerges from both parts.
(Not all polynomials can be factored. Just like some numbers are prime, some polynomials are prime.)
Access these online resources for additional instruction and practice with greatest common factors (GFCs) and factoring by grouping.
Find the Greatest Common Factor of Two or More Expressions
In the following exercises, find the greatest common factor.
Factor the Greatest Common Factor from a Polynomial
In the following exercises, factor the greatest common factor from each polynomial.
Factor by Grouping
In the following exercises, factor by grouping.
Mixed Practice
In the following exercises, factor.
Area of a rectangle The area of a rectangle with length 6 less than the width is given by the expression , where width. Factor the greatest common factor from the polynomial.
Height of a baseball The height of a baseball t seconds after it is hit is given by the expression . Factor the greatest common factor from the polynomial.
The greatest common factor of 36 and 60 is 12. Explain what this means.
Answers will vary.
What is the GCF of ? Write a general rule that tells you how to find the GCF of .
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
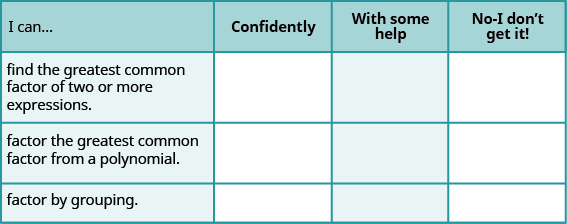
ⓑ If most of your checks were:
…confidently. Congratulations! You have achieved your goals in this section! Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific!
…with some help. This must be addressed quickly as topics you do not master become potholes in your road to success. Math is sequential—every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Who can you ask for help? Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?
…no - I don’t get it! This is critical and you must not ignore it. You need to get help immediately or you will quickly be overwhelmed. See your instructor as soon as possible to discuss your situation. Together you can come up with a plan to get you the help you need.

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?