| << Chapter < Page | Chapter >> Page > |
Before you get started, take this readiness quiz.
We will solve percent equations using the methods we used to solve equations with fractions or decimals. Without the tools of algebra, the best method available to solve percent problems was by setting them up as proportions. Now as an algebra student, you can just translate English sentences into algebraic equations and then solve the equations.
We can use any letter you like as a variable, but it is a good idea to choose a letter that will remind us of what you are looking for. We must be sure to change the given percent to a decimal when we put it in the equation.
Translate and solve: What number is 35% of 90?
 | |
| Translate into algebra. Let = the number. |
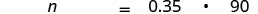 |
| Remember "of" means multiply, "is" means equals. | |
| Multiply. |
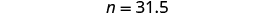 |
| is of |
We must be very careful when we translate the words in the next example. The unknown quantity will not be isolated at first, like it was in [link] . We will again use direct translation to write the equation.
Translate and solve: 6.5% of what number is $1.17?
 | |
| Translate. Let the number. |
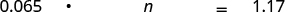 |
| Multiply. |
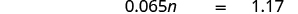 |
| Divide both sides by 0.065 and simplify. |
 |
| of is |
In the next example, we are looking for the percent.
Translate and solve: 144 is what percent of 96?
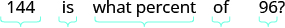 | |
| Translate into algebra. Let the percent. |
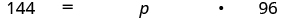 |
| Multiply. |
 |
| Divide by 96 and simplify. |
 |
| Convert to percent. |
 |
| is of |
Note that we are asked to find percent, so we must have our final result in percent form.
Many applications of percent —such as tips, sales tax, discounts, and interest—occur in our daily lives. To solve these applications we’ll translate to a basic percent equation, just like those we solved in previous examples. Once we translate the sentence into a percent equation, we know how to solve it.
We will restate the problem solving strategy we used earlier for easy reference.

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?