| << Chapter < Page | Chapter >> Page > |
Graph the line passing through the point whose slope is
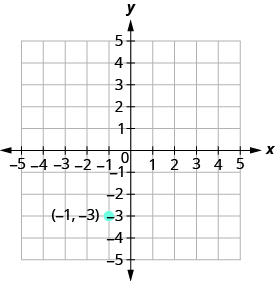
Plot the given point.
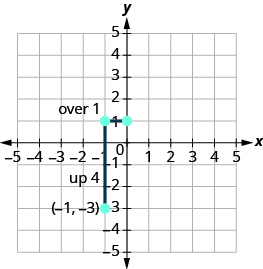
Count the rise and run and mark the second point.
Connect the two points with a line.
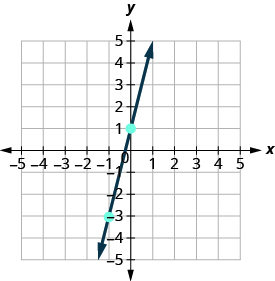
You can check your work by finding a third point. Since the slope is , it can be written as . Go back to and count out the rise, , and the run, .
At the beginning of this section, we said there are many applications of slope in the real world. Let’s look at a few now.
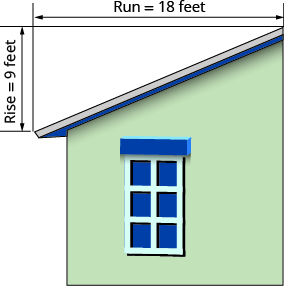
The ‘pitch’ of a building’s roof is the slope of the roof. Knowing the pitch is important in climates where there is heavy snowfall. If the roof is too flat, the weight of the snow may cause it to collapse. What is the slope of the roof shown?
Have you ever thought about the sewage pipes going from your house to the street? They must slope down inch per foot in order to drain properly. What is the required slope?

The pipe drops 1 inch for every 48 inches of horizontal run.
Access these online resources for additional instruction and practice with understanding slope of a line.
Use Geoboards to Model Slope
In the following exercises, find the slope modeled on each geoboard.
In the following exercises, model each slope. Draw a picture to show your results.
Use to find the Slope of a Line from its Graph
In the following exercises, find the slope of each line shown.
Find the Slope of Horizontal and Vertical Lines

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?