7.5 General strategy for factoring polynomials  (Page 2/2)

Solution

Is there a GCF?	No.
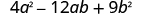Is it a binomial, trinomial, or are there more terms?
Trinomial with $a\ne 1$ . But the first term is a   perfect square.
Is the last term a perfect square?	Yes.
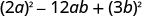Does it fit the pattern, $a^2-2ab+b^2?$	Yes.
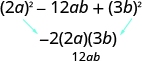Write it as a square.
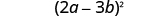Check your answer.
Is the expression factored completely?
Yes.
The binomial is not a difference of squares.
Multiply.
${(2a-3b)}^2$
${\left(2a\right)}^2-2\cdot 2a\cdot 3b+{\left(3b\right)}^2$
$4a^2-12ab+9b^2✓$

Solution

$\begin{array}{ccccccc}\text{Is there a GCF?}\hfill & & & \text{Yes, 6.}\hfill & & & \hfill 6y^2-18y-60\hfill \\ \text{Factor out the GCF.}\hfill & & & \text{Trinomial with leading coefficient 1.}\hfill & & & \hfill 6\left(y^2-3y-10\right)\hfill \\ \begin{array}{c}\text{In the parentheses, is it a binomial, trinomial,}\hfill \\ \text{or are there more terms?}\hfill \end{array}\hfill & & & & & & \\ \text{“Undo” FOIL.}\hfill & & & \hfill 6\left(y\right)\left(y\right)\hfill & & & \hfill 6\left(y+2\right)\left(y-5\right)\hfill \\ \\ \\ \text{Check your answer.}\hfill & & & & & & \\ \text{Is the expression factored completely?}\hfill & & & & & & \hfill \text{Yes.}\hfill \\ \text{Neither binomial is a difference of squares.}\hfill & & & & & & \\ \text{Multiply.}\hfill & & & & & & \\ \\ \\ 6\left(y+2\right)\left(y-5\right)\hfill & & & & & & \\ 6\left(y^2-5y+2y-10\right)\hfill & & & & & & \\ 6\left(y^2-3y-10\right)\hfill & & & & & & \\ 6y^2-18y-60✓\hfill & & & \end{array}$

Solution

Is there a GCF?	Yes, 3.	$24x^3+81$
Factor it out.		$3(8x^3+27)$
In the parentheses, is it a binomial, trinomial, or are there more than three terms?	Binomial.
Is it a sum or difference?	Sum.
Of squares or cubes?	Sum of cubes.
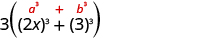Write it using the sum of cubes pattern.
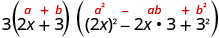Is the expression factored completely?	Yes.	$3(2x+3)(4x^2-6x+9)$
Check by multiplying.		We leave the check to you.

Solution

$\begin{array}{ccccccc}\text{Is there a GCF?}\hfill & & & \text{Yes, 2.}\hfill & & & \hfill 2x^4-32\hfill \\ \text{Factor it out.}\hfill & & & & & & \hfill 2\left(x^4-16\right)\hfill \\ \text{In the parentheses, is it a binomial, trinomial,}\hfill & & & & & & \\ \text{or are there more than three terms?}\hfill & & & \text{Binomial.}\hfill & & & \\ \text{Is it a sum or difference?}\hfill & & & \text{Yes.}\hfill & & & \\ \text{Of squares or cubes?}\hfill & & & \text{Difference of squares.}\hfill & & & \hfill 2\left({\left(x^2\right)}^2-{\left(4\right)}^2\right)\hfill \\ \text{Write it as a product of conjugates.}\hfill & & & & & & \hfill 2\left(x^2-4\right)\left(x^2+4\right)\hfill \\ \text{The first binomial is again a difference of squares.}\hfill & & & & & & \hfill 2\left({\left(x\right)}^2-{\left(2\right)}^2\right)\left(x^2+4\right)\hfill \\ \text{Write it as a product of conjugates.}\hfill & & & & & & \hfill 2\left(x-2\right)\left(x+2\right)\left(x^2+4\right)\hfill \\ \text{Is the expression factored completely?}\hfill & & & \text{Yes.}\hfill & & & \\ \\ \\ \text{None of these binomials is a difference of squares.}\hfill & & & & & & \\ \text{Check your answer.}\hfill & & & & & & \\ \\ \\ \text{Multiply.}\hfill & & & & & & \\ \\ \\ \\ \\ \\ \begin{array}{c}2(x-2)(x+2)(x^2+4)\hfill \\ 2(x^2-4)(x^2+4)\hfill \\ 2(x^4-16)\hfill \\ 2x^4-32✓\hfill \end{array}\hfill & & & & & & \end{array}$

Solution

$\begin{array}{ccccccc}\text{Is there a GCF?}\hfill & & & \text{Yes, 3.}\hfill & & & \hfill 3x^2+6bx-3ax-6ab\hfill \\ \\ \\ \text{Factor out the GCF.}\hfill & & & & & & \hfill 3\left(x^2+2bx-ax-2ab\right)\hfill \\ \\ \\ \text{In the parentheses, is it a binomial, trinomial,}\hfill & & & \text{More than 3}\hfill & & & \\ \text{or are there more terms?}\hfill & & & \text{terms.}\hfill & & & \\ \\ \\ \text{Use grouping.}\hfill & & & & & & \hfill 3\left[x\left(x+2b\right)-a\left(x+2b\right)\right]\hfill \\ & & & & & & \hfill 3\left(x+2b\right)\left(x-a\right)\hfill \\ \text{Check your answer.}\hfill & & & & & & \\ \\ \\ \text{Is the expression factored completely? Yes.}\hfill & & & & & & \\ \text{Multiply.}\hfill & & & & & & \\ 3\left(x+2b\right)\left(x-a\right)\hfill & & & & & & \\ 3\left(x^2-ax+2bx-2ab\right)\hfill & & & & & & \\ 3x^2-3ax+6bx-6ab✓\hfill & & & & & & \end{array}$

Solution

$\begin{array}{ccccccc}\text{Is there a GCF?}\hfill & & & \text{Yes, 2.}\hfill & & & \hfill 10x^2-34x-24\hfill \\ \\ \\ \text{Factor out the GCF.}\hfill & & & & & & \hfill 2\left(5x^2-17x-12\right)\hfill \\ \\ \\ \text{In the parentheses, is it a binomial, trinomial,}\hfill & & & \hfill \text{Trinomial with}\hfill & & & \\ \text{or are there more than three terms?}\hfill & & & a\ne 1.\hfill & & & \\ \\ \\ \text{Use trial and error or the “ac” method.}\hfill & & & & & & \hfill 2\underset{}{(5x^2}-17x\underset{}{\mathrm{-12})}\hfill \\ & & & & & & \hfill 2\left(5x+3\right)\left(x-4\right)\hfill \\ \\ \\ \begin{array}{c}\text{Check your answer. Is the expression factored}\hfill \\ \text{completely? Yes.}\hfill \end{array}\hfill & & & & & & \\ \\ \\ \text{Multiply.}\hfill & & & & & & \\ 2\left(5x+3\right)\left(x-4\right)\hfill & & & & & & \\ 2\left(5x^2-20x+3x-12\right)\hfill & & & & & & \\ 2\left(5x^2-17x-12\right)\hfill & & & & & & \\ 10x^2-34x-24✓\hfill & & & & & & \end{array}$