| << Chapter < Page | Chapter >> Page > |
Orlando is mixing nuts and cereal squares to make a party mix. Nuts sell for $7 a pound and cereal squares sell for $4 a pound. Orlando wants to make 30 pounds of party mix at a cost of $6.50 a pound, how many pounds of nuts and how many pounds of cereal squares should he use?
5 pounds cereal squares, 25 pounds nuts
Becca wants to mix fruit juice and soda to make a punch. She can buy fruit juice for $3 a gallon and soda for $4 a gallon. If she wants to make 28 gallons of punch at a cost of $3.25 a gallon, how many gallons of fruit juice and how many gallons of soda should she buy?
21 gallons of fruit punch, 7 gallons of soda
We can also use the mixture model to solve investment problems using simple interest . We have used the simple interest formula, where represented the number of years. When we just need to find the interest for one year, so then
Stacey has $20,000 to invest in two different bank accounts. One account pays interest at 3% per year and the other account pays interest at 5% per year. How much should she invest in each account if she wants to earn 4.5% interest per year on the total amount?
We will fill in a chart to organize our information. We will use the simple interest formula to find the interest earned in the different accounts.
The interest on the mixed investment will come from adding the interest from the account earning 3% and the interest from the account earning 5% to get the total interest on the $20,000.
The amount invested is the principal for each account.
We enter the interest rate for each account.
We multiply the amount invested times the rate to get the interest.
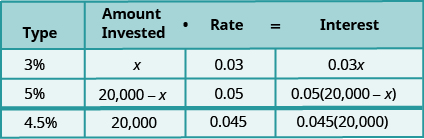
Notice that the total amount invested, 20,000, is the sum of the amount invested at 3% and the amount invested at 5%. And the total interest,
is the sum of the interest earned in the 3% account and the interest earned in the 5% account.
As with the other mixture applications, the last column in the table gives us the equation to solve.
| Write the equation from the interest earned.
Solve the equation. |
amount invested at 3% |
| Find the amount invested at 5%. |


 |
| Check.
|
|
| Stacey should invest $5,000 in the account that
earns 3% and $15,000 in the account that earns 5%. |
Remy has $14,000 to invest in two mutual funds. One fund pays interest at 4% per year and the other fund pays interest at 7% per year. How much should she invest in each fund if she wants to earn 6.1% interest on the total amount?
$4,200 at 4%, $9,800 at 7%
Marco has $8,000 to save for his daughter’s college education. He wants to divide it between one account that pays 3.2% interest per year and another account that pays 8% interest per year. How much should he invest in each account if he wants the interest on the total investment to be 6.5%?
$2,500 at 3.2%, $5,500 at 8%

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?