| << Chapter < Page | Chapter >> Page > |
It is important to remember that sums of squares do not factor into a product of binomials . There are no binomial factors that multiply together to get a sum of squares. After removing any GCF, the expression is prime!
Don’t forget that 1 is a perfect square. We’ll need to use that fact in the next example.
Factor: .
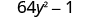 | |
| Is this a difference? Yes. |
 |
| Are the first and last terms perfect squares? | |
| Yes - write them as squares. |
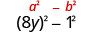 |
| Factor as the product of conjugates. |
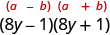 |
| Check by multiplying. | |
The binomial in the next example may look “backwards,” but it’s still the difference of squares.
Factor: .
Be careful not to rewrite the original expression as .
Factor on your own and then notice how the result differs from .
To completely factor the binomial in the next example, we’ll factor a difference of squares twice!
As always, you should look for a common factor first whenever you have an expression to factor. Sometimes a common factor may “disguise” the difference of squares and you won’t recognize the perfect squares until you factor the GCF.
There is another special pattern for factoring, one that we did not use when we multiplied polynomials. This is the pattern for the sum and difference of cubes. We will write these formulas first and then check them by multiplication.
We’ll check the first pattern and leave the second to you.
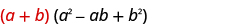 | |
| Distribute. |
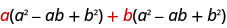 |
| Multiply. | |
| Combine like terms. |

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?