1. Home
  2. Elementary algebra
  3. Systems of linear equations
  4. Solve systems of equations by

5.1 Solve systems of equations by graphing  (Page 4/14)

<< Chapter < Page
  Elementary algebra     Page 4 / 14
Chapter >> Page >

Coincident lines

Coincident lines have the same slope and same y -intercept.

 

Determine the number of solutions of a linear system

There will be times when we will want to know how many solutions there will be to a system of linear equations, but we might not actually have to find the solution. It will be helpful to determine this without graphing.

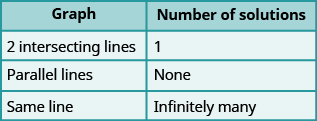
We have seen that two lines in the same plane must either intersect or are parallel. The systems of equations in [link] through [link] all had two intersecting lines. Each system had one solution.

A system with parallel lines, like [link] , has no solution. What happened in [link] ? The equations have coincident lines    , and so the system had infinitely many solutions.

We’ll organize these results in [link] below:

This table has two columns and four rows. The first row labels each column “Graph” and “Number of solutions.” Under “Graph” are “2 intersecting lines,” “Parallel lines,” and “Same line.” Under “Number of solutions” are “1,” “None,” and “Infinitely many.”

Parallel lines have the same slope but different y -intercepts. So, if we write both equations in a system of linear equations in slope–intercept form, we can see how many solutions there will be without graphing! Look at the system we solved in [link] .

{ y = 1 2 x − 3 x − 2 y = 4 The first line is in slope–intercept form. If we solve the second equation for y , we get y = 1 2 x − 3 x − 2 y = 4 −2 y = − x + 4 y = 1 2 x − 2 m = 1 2 , b = −3 m = 1 2 , b = −2

The two lines have the same slope but different y -intercepts. They are parallel lines.

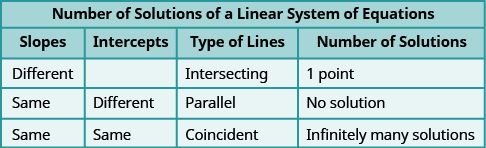
[link] shows how to determine the number of solutions of a linear system by looking at the slopes and intercepts.

This table is entitled “Number of Solutions of a Linear System of Equations.” There are four columns. The columns are labeled, “Slopes,” “Intercepts,” “Type of Lines,” “Number of Solutions.” Under “Slopes” are “Different,” “Same,” and “Same.” Under “Intercepts,” the first cell is blank, then the words “Different” and “Same” appear. Under “Types of Lines” are the words, “Intersecting,” “Parallel,” and “Coincident.” Under “Number of Solutions” are “1 point,” “No Solution,” and “Infinitely many solutions.”

Let’s take one more look at our equations in [link] that gave us parallel lines.

{ y = 1 2 x − 3 x − 2 y = 4

When both lines were in slope-intercept form we had:

y = 1 2 x − 3 y = 1 2 x − 2

Do you recognize that it is impossible to have a single ordered pair ( x , y ) that is a solution to both of those equations?

We call a system of equations like this an inconsistent system . It has no solution.

A system of equations that has at least one solution is called a consistent system    .

Consistent and inconsistent systems

A consistent system    of equations is a system of equations with at least one solution.

An inconsistent system    of equations is a system of equations with no solution.

We also categorize the equations in a system of equations by calling the equations independent or dependent . If two equations are independent equations    , they each have their own set of solutions. Intersecting lines and parallel lines are independent.

If two equations are dependent, all the solutions of one equation are also solutions of the other equation. When we graph two dependent equations    , we get coincident lines.

Independent and dependent equations

Two equations are independent if they have different solutions.

Two equations are dependent if all the solutions of one equation are also solutions of the other equation.

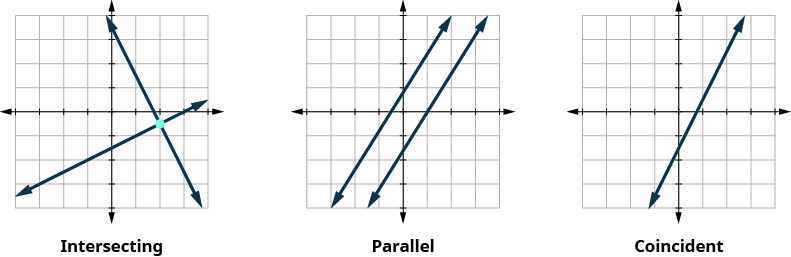
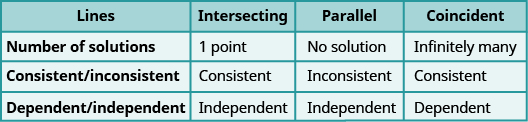
Let’s sum this up by looking at the graphs of the three types of systems. See [link] and [link] .

This figure shows three x y coordinate planes in a horizontal row. The first shows two lines intersecting. The second shows two parallel lines. The third shows two coincident lines.
This table has four columns and four rows. The columns are labeled, “Lines,” “Intersecting,” “Parallel,” and “Coincident.” In the first row under the labeled column “lines” it reads “Number of solutions.” Reading across, it tell us that an intersecting line contains 1 point, a parallel line provides no solution, and a coincident line has infinitely many solutions. A consistent/inconsistent line has consistent lines if they are intersecting, inconsistent lines if they are parallel and consistent if the lines are coincident. Finally, dependent and independent lines are considered independent if the lines intersect, they are also independent if the lines are parallel, and they are dependent if the lines are coincident.

Without graphing, determine the number of solutions and then classify the system of equations: { y = 3 x − 1 6 x − 2 y = 12 .

Solution

We will compare the slopes and intercepts of the two lines. The first equation is already in slope-intercept form. Write the second equation in slope–intercept form. { y = 3 x − 1 6 x − 2 y = 12 y = 3 x − 1 6 x − 2 y = 12 −2 y = −6 x + 12 −2 y −2 = −6 x + 12 −2 Find the slope and intercept of each line. y = 3 x − 6 y = 3 x − 1 y = 3 x − 6 m = 3 m = 3 b = −1 b = −6 Since the slopes are the same and y -intercepts are different, the lines are parallel.

A system of equations whose graphs are parallel lines has no solution and is inconsistent and independent.

Got questions? Get instant answers now!
Got questions? Get instant answers now!

Questions & Answers

A golfer on a fairway is 70 m away from the green, which sits below the level of the fairway by 20 m. If the golfer hits the ball at an angle of 40° with an initial speed of 20 m/s, how close to the green does she come?
Aislinn Reply
cm
tijani
what is titration
John Reply
what is physics
Siyaka Reply
A mouse of mass 200 g falls 100 m down a vertical mine shaft and lands at the bottom with a speed of 8.0 m/s. During its fall, how much work is done on the mouse by air resistance
Jude Reply
Can you compute that for me. Ty
Jude
what is the dimension formula of energy?
David Reply
what is viscosity?
David
what is inorganic
emma Reply
what is chemistry
Youesf Reply
what is inorganic
emma
Chemistry is a branch of science that deals with the study of matter,it composition,it structure and the changes it undergoes
Adjei
please, I'm a physics student and I need help in physics
Adjanou
chemistry could also be understood like the sexual attraction/repulsion of the male and female elements. the reaction varies depending on the energy differences of each given gender. + masculine -female.
Pedro
A ball is thrown straight up.it passes a 2.0m high window 7.50 m off the ground on it path up and takes 1.30 s to go past the window.what was the ball initial velocity
Krampah Reply
2. A sled plus passenger with total mass 50 kg is pulled 20 m across the snow (0.20) at constant velocity by a force directed 25° above the horizontal. Calculate (a) the work of the applied force, (b) the work of friction, and (c) the total work.
Sahid Reply
you have been hired as an espert witness in a court case involving an automobile accident. the accident involved car A of mass 1500kg which crashed into stationary car B of mass 1100kg. the driver of car A applied his brakes 15 m before he skidded and crashed into car B. after the collision, car A s
Samuel Reply
can someone explain to me, an ignorant high school student, why the trend of the graph doesn't follow the fact that the higher frequency a sound wave is, the more power it is, hence, making me think the phons output would follow this general trend?
Joseph Reply
Nevermind i just realied that the graph is the phons output for a person with normal hearing and not just the phons output of the sound waves power, I should read the entire thing next time
Joseph
Follow up question, does anyone know where I can find a graph that accuretly depicts the actual relative "power" output of sound over its frequency instead of just humans hearing
Joseph
"Generation of electrical energy from sound energy | IEEE Conference Publication | IEEE Xplore" ***ieeexplore.ieee.org/document/7150687?reload=true
Ryan
what's motion
Maurice Reply
what are the types of wave
Maurice
answer
Magreth
progressive wave
Magreth
hello friend how are you
Muhammad Reply
fine, how about you?
Mohammed
hi
Mujahid
A string is 3.00 m long with a mass of 5.00 g. The string is held taut with a tension of 500.00 N applied to the string. A pulse is sent down the string. How long does it take the pulse to travel the 3.00 m of the string?
yasuo Reply
Who can show me the full solution in this problem?
Reofrir Reply
Got questions? Join the online conversation and get instant answers!
Jobilize.com Reply
<< Chapter < Page Page > Chapter >>
Practice Key Terms 7

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Elementary algebra. OpenStax CNX. Jan 18, 2017 Download for free at http://cnx.org/content/col12116/1.2
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Elementary algebra' conversation and receive update notifications?

Ask