| << Chapter < Page | Chapter >> Page > |
Fill in for each of the following pairs of numbers:
ⓐ ⓑ ⓒ ⓓ
ⓐ
ⓑ
ⓒ
ⓓ
Fill in<,>, or
for each of the following pairs of numbers:
ⓐ
ⓑ
ⓒ
ⓓ
ⓐ > ⓑ > ⓒ < ⓓ >
Fill in<,>, or
for each of the following pairs of numbers:
ⓐ
ⓑ
ⓒ
ⓓ
ⓐ > ⓑ > ⓒ > ⓓ <
We now add absolute value bars to our list of grouping symbols. When we use the order of operations, first we simplify inside the absolute value bars as much as possible, then we take the absolute value of the resulting number.
In the next example, we simplify the expressions inside absolute value bars first, just like we do with parentheses.
Evaluate: ⓐ ⓑ ⓒ ⓓ
ⓐ
 |
 |
| Take the absolute value. | 35 |
 |
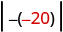 |
| Simplify. | |
| Take the absolute value. | 20 |
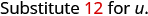 |
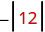 |
| Take the absolute value. |
 |
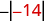 |
| Take the absolute value. |
Most students are comfortable with the addition and subtraction facts for positive numbers. But doing addition or subtraction with both positive and negative numbers may be more challenging.
We will use two color counters to model addition and subtraction of negatives so that you can visualize the procedures instead of memorizing the rules.
We let one color (blue) represent positive. The other color (red) will represent the negatives. If we have one positive counter and one negative counter, the value of the pair is zero. They form a neutral pair. The value of this neutral pair is zero.
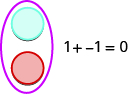
We will use the counters to show how to add the four addition facts using the numbers and
To add we realize that means the sum of 5 and 3.
| We start with 5 positives. |
 |
| And then we add 3 positives. |
 |
| We now have 8 positives. The sum of 5 and 3 is 8. |
 |
Now we will add Watch for similarities to the last example
To add we realize this means the sum of
| We start with 5 negatives. |
 |
| And then we add 3 negatives. |
 |
| We now have 8 negatives. The sum of −5 and −3 is −8. |
 |
In what ways were these first two examples similar?

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?