6.4 Graphs of logarithmic functions (Page 3/8)

<< Chapter < Page

College algebra

Page 3 / 8

Chapter >> Page >

How To

Given a logarithmic function with the form $f (x) = \log_{b} (x),$ graph the function.

Draw and label the vertical asymptote, $x = 0.$
Plot the x- intercept, $(1, 0) .$
Plot the key point $(b, 1) .$
Draw a smooth curve through the points.
State the domain, $(0, \infty),$ the range, $(- \infty, \infty),$ and the vertical asymptote, $x = 0.$

Graphing a logarithmic function with the form f ( x ) = log _b ( x ).

Graph $f (x) = \log_{5} (x) .$ State the domain, range, and asymptote.

Before graphing, identify the behavior and key points for the graph.

Since $b = 5$ is greater than one, we know the function is increasing. The left tail of the graph will approach the vertical asymptote $x = 0,$ and the right tail will increase slowly without bound.
The x -intercept is $(1, 0) .$
The key point $(5, 1)$ is on the graph.
We draw and label the asymptote, plot and label the points, and draw a smooth curve through the points (see [link] ).

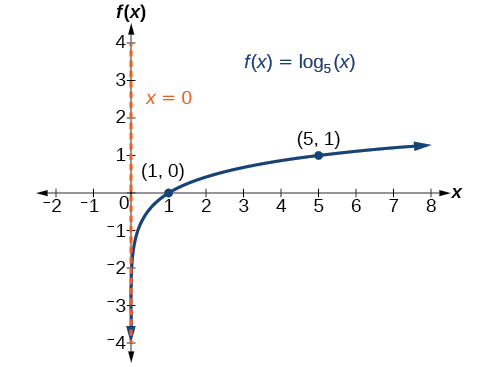
Graph of f(x)=log_5(x) with labeled points at (1, 0) and (5, 1). The y-axis is the asymptote.

The domain is $(0, \infty),$ the range is $(- \infty, \infty),$ and the vertical asymptote is $x = 0.$

Got questions? Get instant answers now!

Try It

Graph $f (x) = \log_{\frac{1}{5}} (x) .$ State the domain, range, and asymptote.

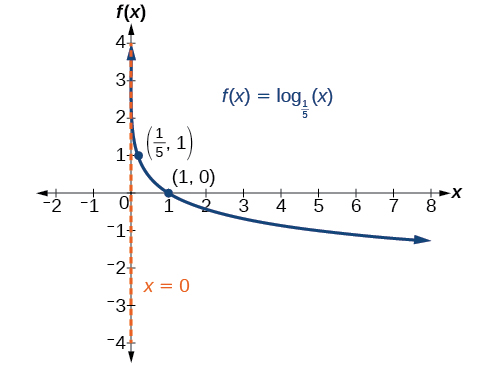
Graph of f(x)=log_(1/5)(x) with labeled points at (1/5, 1) and (1, 0). The y-axis is the asymptote.

The domain is $(0, \infty),$ the range is $(- \infty, \infty),$ and the vertical asymptote is $x = 0.$

Got questions? Get instant answers now!

Graphing transformations of logarithmic functions

As we mentioned in the beginning of the section, transformations of logarithmic graphs behave similarly to those of other parent functions. We can shift, stretch, compress, and reflect the parent function $y = \log_{b} (x)$ without loss of shape.

Graphing a horizontal shift of f ( x ) = log _b ( x )

When a constant $c$ is added to the input of the parent function $f (x) = l o g_{b} (x),$ the result is a horizontal shift $c$ units in the opposite direction of the sign on $c .$ To visualize horizontal shifts, we can observe the general graph of the parent function $f (x) = \log_{b} (x)$ and for $c > 0$ alongside the shift left, $g (x) = \log_{b} (x + c),$ and the shift right, $h (x) = \log_{b} (x - c) .$ See [link] .

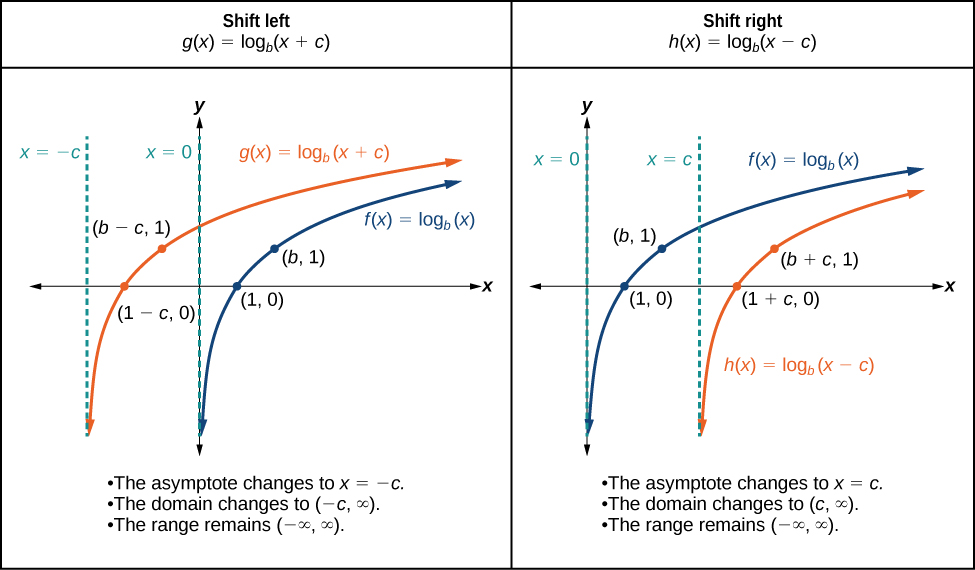
Graph of two functions. The parent function is f(x)=log_b(x), with an asymptote at x=0 and g(x)=log_b(x+c) is the translation function with an asymptote at x=-c. This shows the translation of shifting left.

A General Note

Horizontal shifts of the parent function y = log _b ( x )

For any constant $c,$ the function $f (x) = \log_{b} (x + c)$

shifts the parent function $y = \log_{b} (x)$ left $c$ units if $c > 0.$
shifts the parent function $y = \log_{b} (x)$ right $c$ units if $c < 0.$
has the vertical asymptote $x = - c .$
has domain $(- c, \infty) .$
has range $(- \infty, \infty) .$

How To

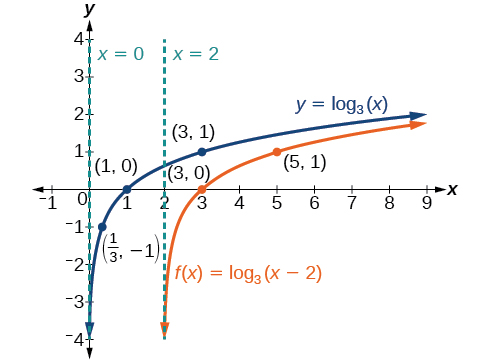
Given a logarithmic function with the form $f (x) = \log_{b} (x + c),$ graph the translation.

Identify the horizontal shift:
1. If $c > 0,$ shift the graph of $f (x) = \log_{b} (x)$ left $c$ units.
2. If $c < 0,$ shift the graph of $f (x) = \log_{b} (x)$ right $c$ units.
Draw the vertical asymptote $x = - c .$
Identify three key points from the parent function. Find new coordinates for the shifted functions by subtracting $c$ from the $x$ coordinate.
Label the three points.
The Domain is $(- c, \infty),$ the range is $(- \infty, \infty),$ and the vertical asymptote is $x = - c .$

Graphing a horizontal shift of the parent function y = log _b ( x )

Sketch the horizontal shift $f (x) = \log_{3} (x - 2)$ alongside its parent function. Include the key points and asymptotes on the graph. State the domain, range, and asymptote.

Since the function is $f (x) = \log_{3} (x - 2),$ we notice $x + (- 2) = x - 2.$

Thus $c = - 2,$ so $c < 0.$ This means we will shift the function $f (x) = \log_{3} (x)$ right 2 units.

The vertical asymptote is $x = - (- 2)$ or $x = 2.$

Consider the three key points from the parent function, $(\frac{1}{3}, −1),$ $(1, 0),$ and $(3, 1) .$

The new coordinates are found by adding 2 to the $x$ coordinates.

Label the points $(\frac{7}{3}, −1),$ $(3, 0),$ and $(5, 1) .$

The domain is $(2, \infty),$ the range is $(- \infty, \infty),$ and the vertical asymptote is $x = 2.$

Graph of two functions. The parent function is y=log_3(x), with an asymptote at x=0 and labeled points at (1/3, -1), (1, 0), and (3, 1).The translation function f(x)=log_3(x-2) has an asymptote at x=2 and labeled points at (3, 0) and (5, 1).

Got questions? Get instant answers now!

Questions & Answers

what is defense mechanism

Chinaza Reply

what is defense mechanisms

Chinaza

I'm interested in biological psychology and cognitive psychology

Tanya Reply

what does preconceived mean

sammie Reply

physiological Psychology

Nwosu Reply

How can I develope my cognitive domain

Amanyire Reply

why is communication effective

Dakolo Reply

Communication is effective because it allows individuals to share ideas, thoughts, and information with others.

effective communication can lead to improved outcomes in various settings, including personal relationships, business environments, and educational settings. By communicating effectively, individuals can negotiate effectively, solve problems collaboratively, and work towards common goals.

it starts up serve and return practice/assessments.it helps find voice talking therapy also assessments through relaxed conversation.

miss

Every time someone flushes a toilet in the apartment building, the person begins to jumb back automatically after hearing the flush, before the water temperature changes. Identify the types of learning, if it is classical conditioning identify the NS, UCS, CS and CR. If it is operant conditioning, identify the type of consequence positive reinforcement, negative reinforcement or punishment

Wekolamo Reply

please i need answer

Wekolamo

because it helps many people around the world to understand how to interact with other people and understand them well, for example at work (job).

Manix Reply

Agreed 👍 There are many parts of our brains and behaviors, we really need to get to know. Blessings for everyone and happy Sunday!

ARC

A child is a member of community not society elucidate ?

JESSY Reply

Isn't practices worldwide, be it psychology, be it science. isn't much just a false belief of control over something the mind cannot truly comprehend?

Simon Reply

compare and contrast skinner's perspective on personality development on freud

namakula Reply

Skinner skipped the whole unconscious phenomenon and rather emphasized on classical conditioning

war

explain how nature and nurture affect the development and later the productivity of an individual.

Amesalu Reply

nature is an hereditary factor while nurture is an environmental factor which constitute an individual personality. so if an individual's parent has a deviant behavior and was also brought up in an deviant environment, observation of the behavior and the inborn trait we make the individual deviant.

Samuel

I am taking this course because I am hoping that I could somehow learn more about my chosen field of interest and due to the fact that being a PsyD really ignites my passion as an individual the more I hope to learn about developing and literally explore the complexity of my critical thinking skills

Zyryn Reply

good👍

Jonathan

and having a good philosophy of the world is like a sandwich and a peanut butter 👍

Jonathan

generally amnesi how long yrs memory loss

Kelu Reply

interpersonal relationships

Abdulfatai Reply

Got questions? Join the online conversation and get instant answers!

Jobilize.com Reply

<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, College algebra. OpenStax CNX. Feb 06, 2015 Download for free at https://legacy.cnx.org/content/col11759/1.3

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'College algebra' conversation and receive update notifications?

Ask

	4 Graphing a horizontal shift of f ( x ) = log b ( x ) By OpenStax Read Online Course
	2 Graphing logarithmic functions By OpenStax Read Online Course
	Tournament Director Quiz By Eddie Unverzagt Start Quiz
	38 Biology 38 The Musculoskeletal System MCQ By OpenStax Start Quiz
©flickr:	Health Reviewer MCQ By Edgar Delgado Start Quiz
	16 Dr. Amberg Pharm quiz 2 By Brooke Delaney Start Exam
	American Politics MCQ By Nicole Bartels Start Quiz
	NCE Ch 06 Groups By Anh Dao Start Quiz
©flickr: Miguel	Protozoal and Parasitic Infections By Cath Yu Start Quiz
©flickr: Ruben	Grade 10 Module 2.1 IT Quiz (Part 2) By Christine Zeelie Start Quiz
	Vocabulary Week 1-3 By Rachel Woolard Start Quiz
	3 AP Key Terms 03 Cellular Level of Organization By OpenStax Start Key Terms

6.4 Graphs of logarithmic functions (Page 3/8)

Graphing a logarithmic function with the form f ( x ) = log b ( x ).

Graphing transformations of logarithmic functions

Graphing a horizontal shift of f ( x ) = log b ( x )

Horizontal shifts of the parent function y = log b ( x )

Graphing a horizontal shift of the parent function y = log b ( x )

Questions & Answers

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Graphing a logarithmic function with the form f ( x ) = log _b ( x ).

Graphing a horizontal shift of f ( x ) = log _b ( x )

Horizontal shifts of the parent function y = log _b ( x )

Graphing a horizontal shift of the parent function y = log _b ( x )