| << Chapter < Page | Chapter >> Page > |
Given a logarithmic function, identify the domain.
What is the domain of
The logarithmic function is defined only when the input is positive, so this function is defined when Solving this inequality,
The domain of is
What is the domain of
The logarithmic function is defined only when the input is positive, so this function is defined when Solving this inequality,
The domain of is
Now that we have a feel for the set of values for which a logarithmic function is defined, we move on to graphing logarithmic functions. The family of logarithmic functions includes the parent function along with all its transformations: shifts, stretches, compressions, and reflections.
We begin with the parent function Because every logarithmic function of this form is the inverse of an exponential function with the form their graphs will be reflections of each other across the line To illustrate this, we can observe the relationship between the input and output values of and its equivalent in [link] .
Using the inputs and outputs from [link] , we can build another table to observe the relationship between points on the graphs of the inverse functions and See [link] .
As we’d expect, the x - and y -coordinates are reversed for the inverse functions. [link] shows the graph of and
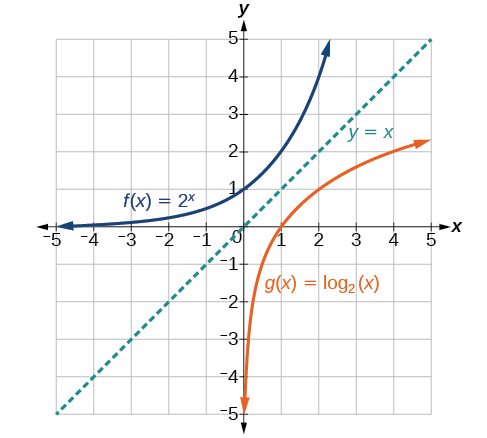
Observe the following from the graph:
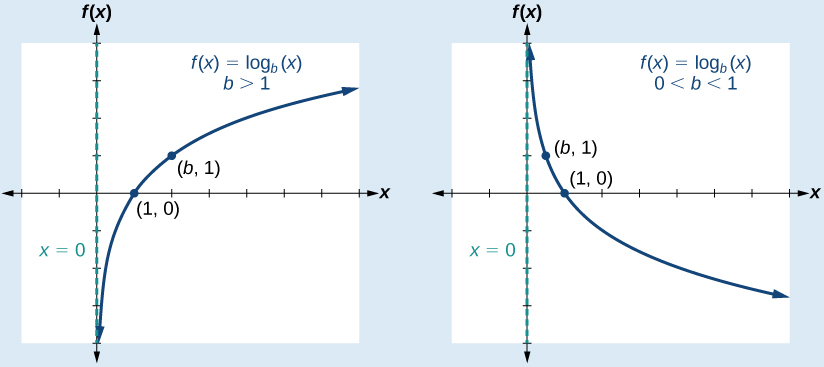
For any real number and constant we can see the following characteristics in the graph of
See [link] .
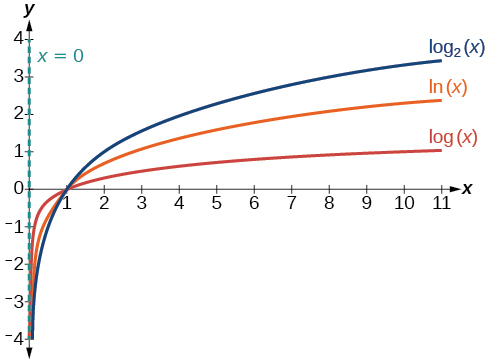
[link] shows how changing the base in can affect the graphs. Observe that the graphs compress vertically as the value of the base increases. ( Note: recall that the function has base

Notification Switch
Would you like to follow the 'College algebra' conversation and receive update notifications?