| << Chapter < Page | Chapter >> Page > |
A mound of gravel is in the shape of a cone with the height equal to twice the radius.

The volume is found using a formula from elementary geometry.
We have written the volume in terms of the radius However, in some cases, we may start out with the volume and want to find the radius. For example: A customer purchases 100 cubic feet of gravel to construct a cone shape mound with a height twice the radius. What are the radius and height of the new cone? To answer this question, we use the formula
This function is the inverse of the formula for in terms of
In this section, we will explore the inverses of polynomial and rational functions and in particular the radical functions we encounter in the process.
Two functions and are inverse functions if for every coordinate pair in there exists a corresponding coordinate pair in the inverse function, In other words, the coordinate pairs of the inverse functions have the input and output interchanged. Only one-to-one functions have inverses. Recall that a one-to-one function has a unique output value for each input value and passes the horizontal line test.
For example, suppose a water runoff collector is built in the shape of a parabolic trough as shown in [link] . We can use the information in the figure to find the surface area of the water in the trough as a function of the depth of the water.
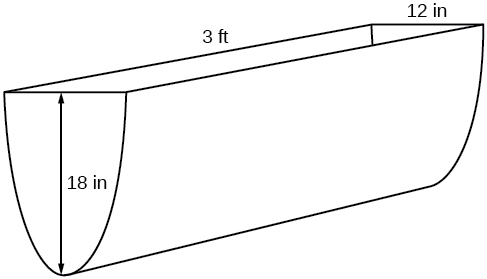
Because it will be helpful to have an equation for the parabolic cross-sectional shape, we will impose a coordinate system at the cross section, with measured horizontally and measured vertically, with the origin at the vertex of the parabola. See [link] .
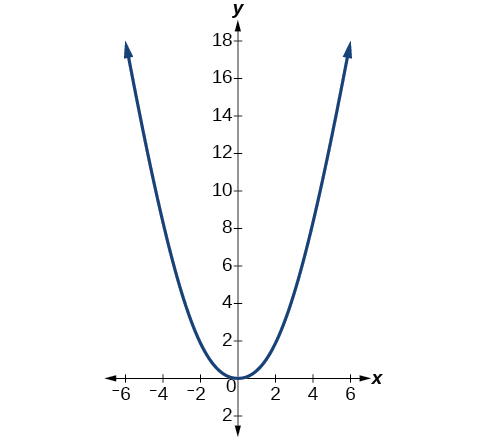
From this we find an equation for the parabolic shape. We placed the origin at the vertex of the parabola, so we know the equation will have form Our equation will need to pass through the point (6, 18), from which we can solve for the stretch factor
Our parabolic cross section has the equation
We are interested in the surface area of the water, so we must determine the width at the top of the water as a function of the water depth. For any depth the width will be given by so we need to solve the equation above for and find the inverse function. However, notice that the original function is not one-to-one, and indeed, given any output there are two inputs that produce the same output, one positive and one negative.
To find an inverse, we can restrict our original function to a limited domain on which it is one-to-one. In this case, it makes sense to restrict ourselves to positive values. On this domain, we can find an inverse by solving for the input variable:
This is not a function as written. We are limiting ourselves to positive values, so we eliminate the negative solution, giving us the inverse function we’re looking for.

Notification Switch
Would you like to follow the 'College algebra' conversation and receive update notifications?