| << Chapter < Page | Chapter >> Page > |
This tells us that has the same sine and cosine values as except for the sign.
Since is in the second quadrant, the x -coordinate of the point on the circle is negative, so the cosine value is negative. The y -coordinate is positive, so the sine value is positive.
Now that we have learned how to find the cosine and sine values for special angles in the first quadrant, we can use symmetry and reference angles to fill in cosine and sine values for the rest of the special angles on the unit circle . They are shown in [link] . Take time to learn the coordinates of all of the major angles in the first quadrant.
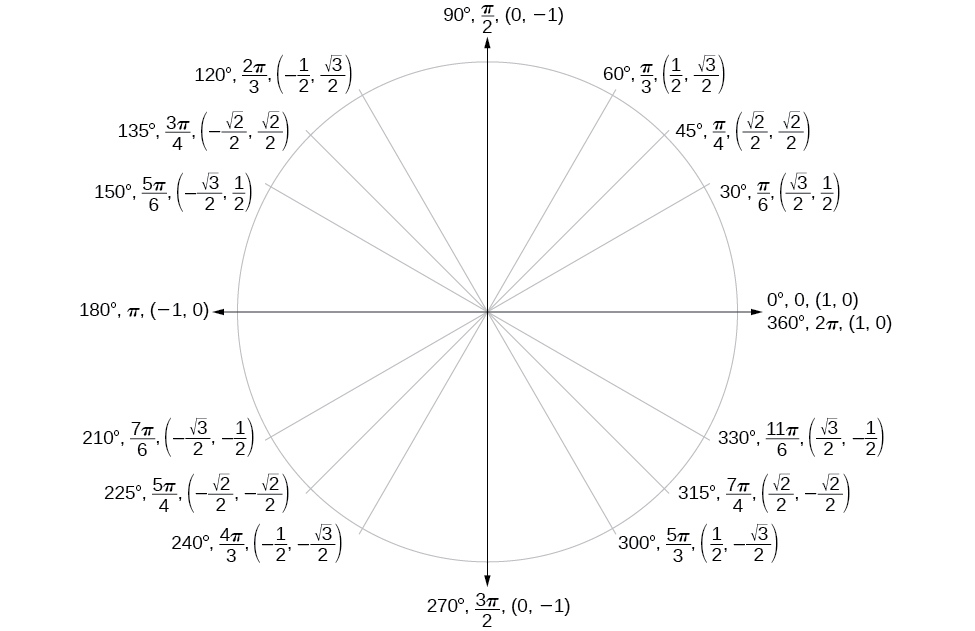
In addition to learning the values for special angles, we can use reference angles to find coordinates of any point on the unit circle, using what we know of reference angles along with the identities
First we find the reference angle corresponding to the given angle. Then we take the sine and cosine values of the reference angle, and give them the signs corresponding to the y - and x -values of the quadrant.
Given the angle of a point on a circle and the radius of the circle, find the coordinates of the point.
Find the coordinates of the point on the unit circle at an angle of
We know that the angle is in the third quadrant.
First, let’s find the reference angle by measuring the angle to the x -axis. To find the reference angle of an angle whose terminal side is in quadrant III, we find the difference of the angle and
Next, we will find the cosine and sine of the reference angle.
We must determine the appropriate signs for x and y in the given quadrant. Because our original angle is in the third quadrant, where both and are negative, both cosine and sine are negative.
Now we can calculate the coordinates using the identities and
The coordinates of the point are on the unit circle.
Find the coordinates of the point on the unit circle at an angle of

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?