13.2 Arithmetic sequences  (Page 3/8)

Using explicit formulas for arithmetic sequences

We can think of an arithmetic sequence    as a function on the domain of the natural numbers; it is a linear function because it has a constant rate of change. The common difference is the constant rate of change, or the slope of the function. We can construct the linear function if we know the slope and the vertical intercept.

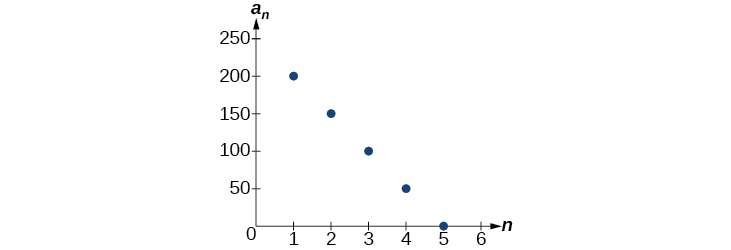
To find the y -intercept of the function, we can subtract the common difference from the first term of the sequence. Consider the following sequence.

The common difference is $-50$ , so the sequence represents a linear function with a slope of $-50$ . To find the $y$ -intercept, we subtract $-50$ from $200:200-(-50)=200+50=250$ . You can also find the $y$ -intercept by graphing the function and determining where a line that connects the points would intersect the vertical axis. The graph is shown in [link] .

Recall the slope-intercept form of a line is $y=mx+b.$ When dealing with sequences, we use $a_n$ in place of $y$ and $n$ in place of $x.$ If we know the slope and vertical intercept of the function, we can substitute them for $m$ and $b$ in the slope-intercept form of a line. Substituting $-50$ for the slope and $250$ for the vertical intercept, we get the following equation:

We do not need to find the vertical intercept to write an explicit formula    for an arithmetic sequence. Another explicit formula for this sequence is $a_n=200-50(n-1)$ , which simplifies to $a_n=-50n+250.$

Finding the number of terms in a finite arithmetic sequence

Explicit formulas can be used to determine the number of terms in a finite arithmetic sequence. We need to find the common difference, and then determine how many times the common difference must be added to the first term to obtain the final term of the sequence.