| << Chapter < Page | Chapter >> Page > |
Use the graph of the function of degree 5 in [link] to identify the zeros of the function and their multiplicities.
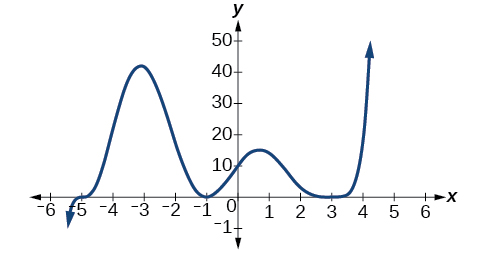
The graph has a zero of –5 with multiplicity 1, a zero of –1 with multiplicity 2, and a zero of 3 with even multiplicity.
As we have already learned, the behavior of a graph of a polynomial function of the form
will either ultimately rise or fall as increases without bound and will either rise or fall as decreases without bound. This is because for very large inputs, say 100 or 1,000, the leading term dominates the size of the output. The same is true for very small inputs, say –100 or –1,000.
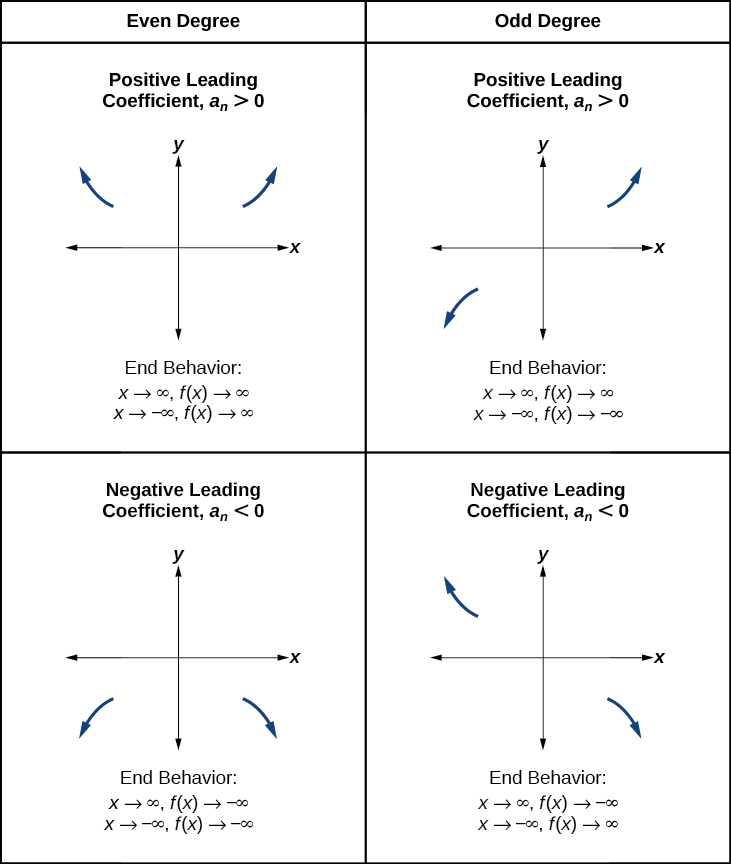
Recall that we call this behavior the end behavior of a function. As we pointed out when discussing quadratic equations, when the leading term of a polynomial function, is an even power function, as increases or decreases without bound, increases without bound. When the leading term is an odd power function, as decreases without bound, also decreases without bound; as increases without bound, also increases without bound. If the leading term is negative, it will change the direction of the end behavior. [link] summarizes all four cases.
In addition to the end behavior, recall that we can analyze a polynomial function’s local behavior. It may have a turning point where the graph changes from increasing to decreasing (rising to falling) or decreasing to increasing (falling to rising). Look at the graph of the polynomial function in [link] . The graph has three turning points.
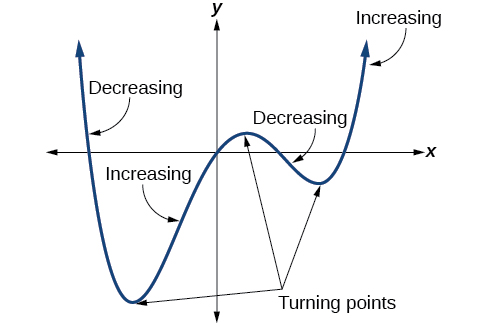
This function is a 4 th degree polynomial function and has 3 turning points. The maximum number of turning points of a polynomial function is always one less than the degree of the function.
A turning point is a point of the graph where the graph changes from increasing to decreasing (rising to falling) or decreasing to increasing (falling to rising).
A polynomial of degree will have at most turning points.
Find the maximum number of turning points of each polynomial function.
First, rewrite the polynomial function in descending order:
Identify the degree of the polynomial function. This polynomial function is of degree 5.
The maximum number of turning points is
First, identify the leading term of the polynomial function if the function were expanded.
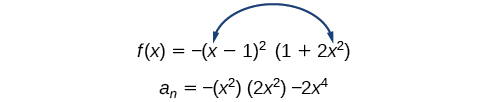
Then, identify the degree of the polynomial function. This polynomial function is of degree 4.
The maximum number of turning points is
We can use what we have learned about multiplicities, end behavior, and turning points to sketch graphs of polynomial functions. Let us put this all together and look at the steps required to graph polynomial functions.
Given a polynomial function, sketch the graph.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?