6.2 Graphs of exponential functions  (Page 2/6)

Sketching the graph of an exponential function of the form f ( x ) = b ^x

Sketch a graph of $f(x)={0.25}^x.$ State the domain, range, and asymptote.

Before graphing, identify the behavior and create a table of points for the graph.

• Since $b=0.25$ is between zero and one, we know the function is decreasing. The left tail of the graph will increase without bound, and the right tail will approach the asymptote $y=0.$
• Create a table of points as in [link] .

  $x$	$-3$	$-2$	$-1$	$0$	$1$	$2$	$3$
  $f(x)={0.25}^x$	$64$	$16$	$4$	$1$	$0.25$	$0.0625$	$0.015625$

• Plot the y -intercept, $\left(0,1\right),$ along with two other points. We can use $\left(-1,4\right)$ and $\left(1,0.25\right).$

Draw a smooth curve connecting the points as in [link] .

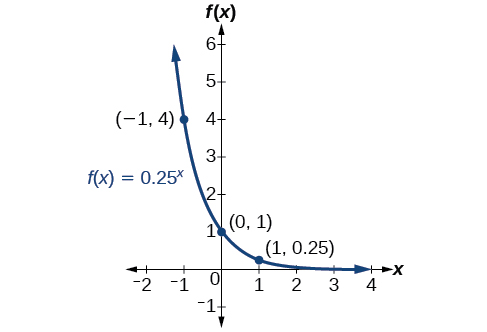
The domain is $\left(-\infty ,\infty \right);$ the range is $\left(0,\infty \right);$ the horizontal asymptote is $y=0.$

Got questions? Get instant answers now!

Got questions? Get instant answers now!

Try It

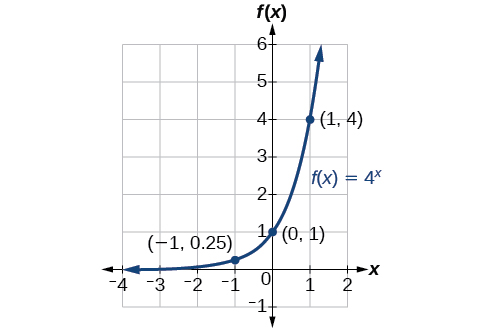
Sketch the graph of $f(x)=4^x.$ State the domain, range, and asymptote.

The domain is $\left(-\infty ,\infty \right);$ the range is $\left(0,\infty \right);$ the horizontal asymptote is $y=0.$

Got questions? Get instant answers now!

Graphing transformations of exponential functions

Transformations of exponential graphs behave similarly to those of other functions. Just as with other parent functions, we can apply the four types of transformations—shifts, reflections, stretches, and compressions—to the parent function $f(x)=b^x$ without loss of shape. For instance, just as the quadratic function maintains its parabolic shape when shifted, reflected, stretched, or compressed, the exponential function also maintains its general shape regardless of the transformations applied.

Graphing a vertical shift

The first transformation occurs when we add a constant $d$ to the parent function $f(x)=b^x,$ giving us a vertical shift     $d$ units in the same direction as the sign. For example, if we begin by graphing a parent function, $f(x)=2^x,$ we can then graph two vertical shifts alongside it, using $d=3:$ the upward shift, $g(x)=2^x+3$ and the downward shift, $h(x)=2^x-3.$ Both vertical shifts are shown in [link] .

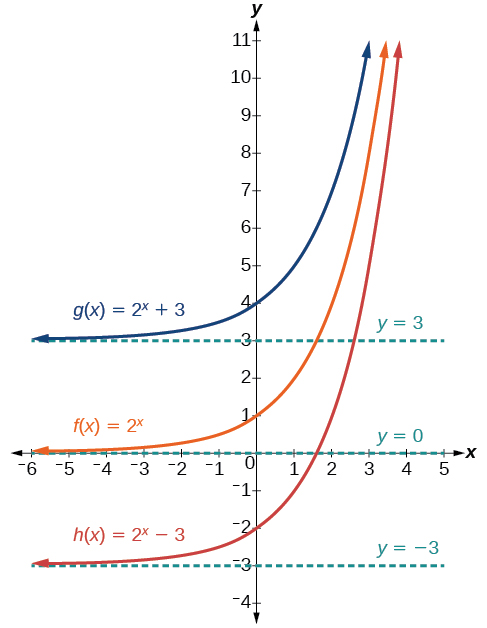
Observe the results of shifting $f(x)=2^x$ vertically:

• The domain, $\left(-\infty ,\infty \right)$ remains unchanged.
• When the function is shifted up $3$ units to $g(x)=2^x+3:$
  • The y- intercept shifts up $3$ units to $\left(0,4\right).$
  • The asymptote shifts up $3$ units to $y=3.$
  • The range becomes $\left(3,\infty \right).$
• When the function is shifted down $3$ units to $h(x)=2^x-3:$
  • The y- intercept shifts down $3$ units to $\left(0,-2\right).$
  • The asymptote also shifts down $3$ units to $y=-3.$
  • The range becomes $\left(-3,\infty \right).$

Graphing a horizontal shift

The next transformation occurs when we add a constant $c$ to the input of the parent function $f(x)=b^x,$ giving us a horizontal shift     $c$ units in the opposite direction of the sign. For example, if we begin by graphing the parent function $f(x)=2^x,$ we can then graph two horizontal shifts alongside it, using $c=3:$ the shift left, $g(x)=2^{x+3},$ and the shift right, $h(x)=2^{x-3}.$ Both horizontal shifts are shown in [link] .

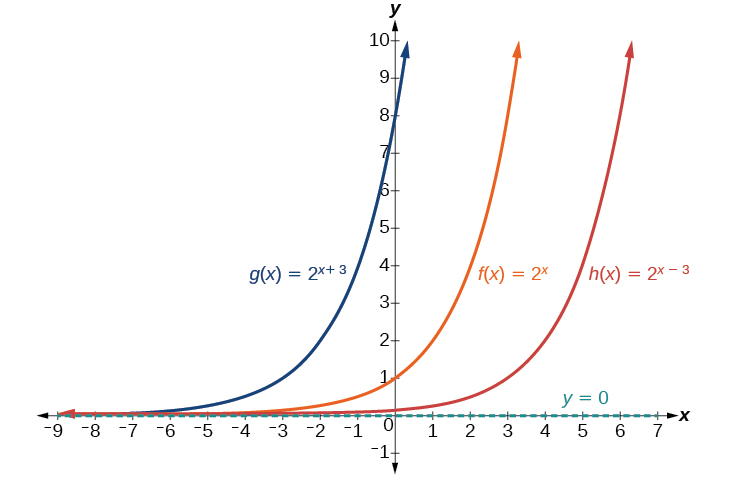
Observe the results of shifting $f(x)=2^x$ horizontally:

• The domain, $\left(-\infty ,\infty \right),$ remains unchanged.
• The asymptote, $y=0,$ remains unchanged.
• The y- intercept shifts such that:
  • When the function is shifted left $3$ units to $g(x)=2^{x+3},$ the y -intercept becomes $\left(0,8\right).$ This is because $2^{x+3}=\left(8\right)2^x,$ so the initial value of the function is $8.$
  • When the function is shifted right $3$ units to $h(x)=2^{x-3},$ the y -intercept becomes $\left(0,\frac{1}{8}\right).$ Again, see that $2^{x-3}=\left(\frac{1}{8}\right)2^x,$ so the initial value of the function is $\frac{1}{8}.$