1.1 Real numbers: algebra essentials  (Page 6/35)

As we can see, neither subtraction nor division is associative.

Distributive property

The distributive property    states that the product of a factor times a sum is the sum of the factor times each term in the sum.

This property combines both addition and multiplication (and is the only property to do so). Let us consider an example.

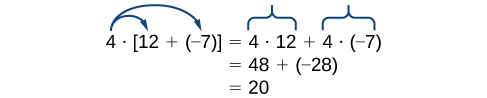
Note that 4 is outside the grouping symbols, so we distribute the 4 by multiplying it by 12, multiplying it by –7, and adding the products.

To be more precise when describing this property, we say that multiplication distributes over addition. The reverse is not true, as we can see in this example.

Multiplication does not distribute over subtraction, and division distributes over neither addition nor subtraction.

A special case of the distributive property occurs when a sum of terms is subtracted.

For example, consider the difference $12-\left(5+3\right).$ We can rewrite the difference of the two terms 12 and $\left(5+3\right)$ by turning the subtraction expression into addition of the opposite. So instead of subtracting $\left(5+3\right),$ we add the opposite.

Now, distribute $\mathrm{-1}$ and simplify the result.

This seems like a lot of trouble for a simple sum, but it illustrates a powerful result that will be useful once we introduce algebraic terms. To subtract a sum of terms, change the sign of each term and add the results. With this in mind, we can rewrite the last example.

Identity properties

The identity property of addition    states that there is a unique number, called the additive identity (0) that, when added to a number, results in the original number.

The identity property of multiplication    states that there is a unique number, called the multiplicative identity (1) that, when multiplied by a number, results in the original number.

For example, we have $\left(\mathrm{-6}\right)+0=\mathrm{-6}$ and $23\cdot 1=23.$ There are no exceptions for these properties; they work for every real number, including 0 and 1.

Inverse properties

The inverse property of addition    states that, for every real number a , there is a unique number, called the additive inverse (or opposite), denoted− a , that, when added to the original number, results in the additive identity, 0.

For example, if $a=\mathrm{-8},$ the additive inverse is 8, since $\left(\mathrm{-8}\right)+8=0.$

The inverse property of multiplication    holds for all real numbers except 0 because the reciprocal of 0 is not defined. The property states that, for every real number a , there is a unique number, called the multiplicative inverse (or reciprocal), denoted $\frac{1}{a},$ that, when multiplied by the original number, results in the multiplicative identity, 1.

For example, if $a=-\frac{2}{3},$ the reciprocal, denoted $\frac{1}{a},$ is $-\frac{3}{2}$ because