| << Chapter < Page | Chapter >> Page > |
A wheelchair ramp that meets the standards of the Americans with Disabilities Act must make an angle with the ground whose tangent is or less, regardless of its length. A tangent represents a ratio, so this means that for every 1 inch of rise, the ramp must have 12 inches of run. Trigonometric functions allow us to specify the shapes and proportions of objects independent of exact dimensions. We have already defined the sine and cosine functions of an angle. Though sine and cosine are the trigonometric functions most often used, there are four others. Together they make up the set of six trigonometric functions. In this section, we will investigate the remaining functions.
We can also define the remaining functions in terms of the unit circle with a point corresponding to an angle of as shown in [link] . As with the sine and cosine, we can use the coordinates to find the other functions.
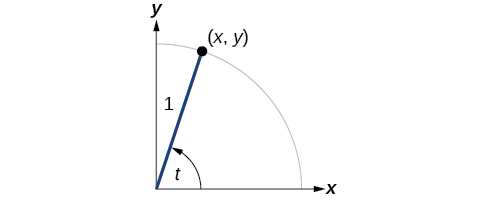
The first function we will define is the tangent. The tangent of an angle is the ratio of the y -value to the x -value of the corresponding point on the unit circle. In [link] , the tangent of angle is equal to Because the y -value is equal to the sine of and the x -value is equal to the cosine of the tangent of angle can also be defined as The tangent function is abbreviated as The remaining three functions can all be expressed as reciprocals of functions we have already defined.
If is a real number and is a point where the terminal side of an angle of radians intercepts the unit circle, then
The point is on the unit circle, as shown in [link] . Find and
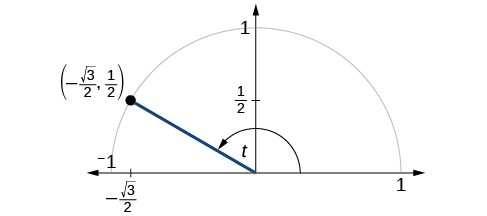
Because we know the coordinates of the point on the unit circle indicated by angle we can use those coordinates to find the six functions:

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?