| << Chapter < Page | Chapter >> Page > |
Reflect the graph of (a) vertically and (b) horizontally.
Reflecting the graph vertically means that each output value will be reflected over the horizontal t- axis as shown in [link] .
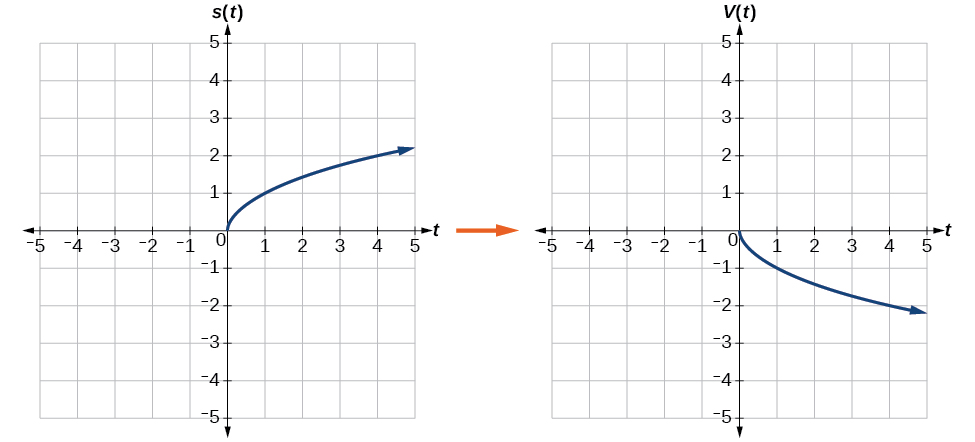
Because each output value is the opposite of the original output value, we can write
Notice that this is an outside change, or vertical shift, that affects the output values, so the negative sign belongs outside of the function.
Reflecting horizontally means that each input value will be reflected over the vertical axis as shown in [link] .
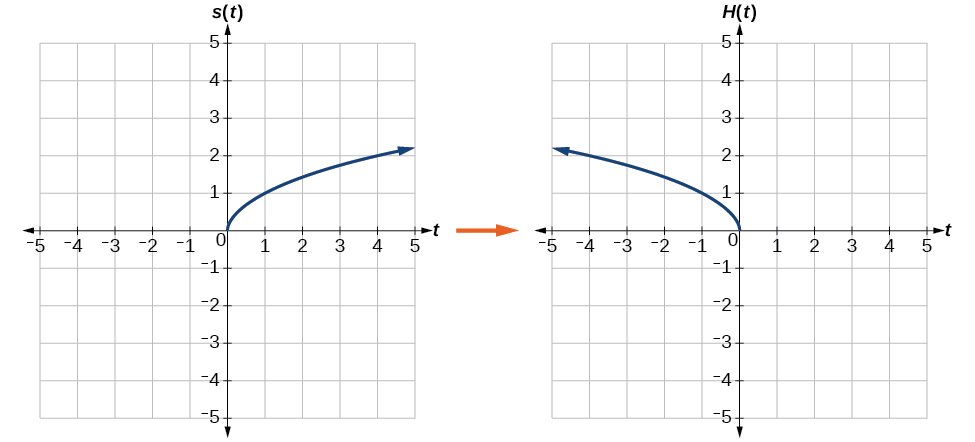
Because each input value is the opposite of the original input value, we can write
Notice that this is an inside change or horizontal change that affects the input values, so the negative sign is on the inside of the function.
Note that these transformations can affect the domain and range of the functions. While the original square root function has domain and range the vertical reflection gives the function the range and the horizontal reflection gives the function the domain
A function is given as [link] . Create a table for the functions below.
| 2 | 4 | 6 | 8 | |
| 1 | 3 | 7 | 11 |
For the negative sign outside the function indicates a vertical reflection, so the x -values stay the same and each output value will be the opposite of the original output value. See [link] .
| 2 | 4 | 6 | 8 | |
| –1 | –3 | –7 | –11 |
For the negative sign inside the function indicates a horizontal reflection, so each input value will be the opposite of the original input value and the values stay the same as the values. See [link] .
| −2 | −4 | −6 | −8 | |
| 1 | 3 | 7 | 11 |
| -2 | 0 | 2 | 4 | |
| -2 | 0 | 2 | 4 | |
| 15 | 10 | 5 | unknown |
A common model for learning has an equation similar to where is the percentage of mastery that can be achieved after practice sessions. This is a transformation of the function shown in [link] . Sketch a graph of
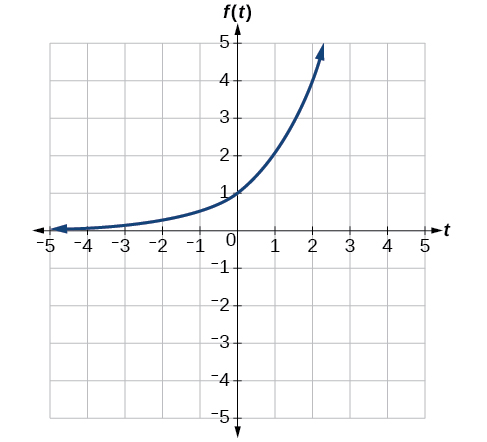
This equation combines three transformations into one equation.
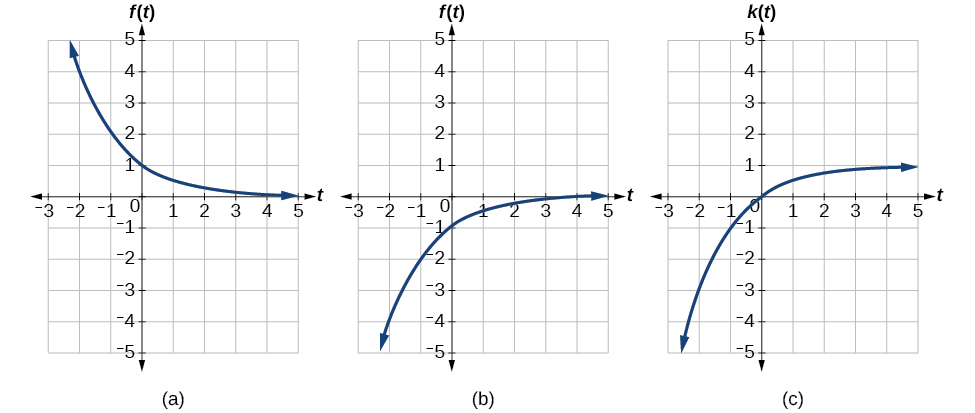
We can sketch a graph by applying these transformations one at a time to the original function. Let us follow two points through each of the three transformations. We will choose the points (0, 1) and (1, 2).
This means that the original points, (0,1) and (1,2) become (0,0) and (-1,-1) after we apply the transformations.
In [link] , the first graph results from a horizontal reflection. The second results from a vertical reflection. The third results from a vertical shift up 1 unit.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?