| << Chapter < Page | Chapter >> Page > |
It takes Andrew 30 min to drive to work in the morning. He drives home using the same route, but it takes 10 min longer, and he averages 10 mi/h less than in the morning. How far does Andrew drive to work?
This is a distance problem, so we can use the formula where distance equals rate multiplied by time. Note that when rate is given in mi/h, time must be expressed in hours. Consistent units of measurement are key to obtaining a correct solution.
First, we identify the known and unknown quantities. Andrew’s morning drive to work takes 30 min, or h at rate His drive home takes 40 min, or h, and his speed averages 10 mi/h less than the morning drive. Both trips cover distance A table, such as [link] , is often helpful for keeping track of information in these types of problems.
| To Work | |||
| To Home |
Write two equations, one for each trip.
As both equations equal the same distance, we set them equal to each other and solve for r .
We have solved for the rate of speed to work, 40 mph. Substituting 40 into the rate on the return trip yields 30 mi/h. Now we can answer the question. Substitute the rate back into either equation and solve for d.
The distance between home and work is 20 mi.
On Saturday morning, it took Jennifer 3.6 h to drive to her mother’s house for the weekend. On Sunday evening, due to heavy traffic, it took Jennifer 4 h to return home. Her speed was 5 mi/h slower on Sunday than on Saturday. What was her speed on Sunday?
45 mi/h
The perimeter of a rectangular outdoor patio is ft. The length is ft greater than the width. What are the dimensions of the patio?
The perimeter formula is standard: We have two unknown quantities, length and width. However, we can write the length in terms of the width as Substitute the perimeter value and the expression for length into the formula. It is often helpful to make a sketch and label the sides as in [link] .
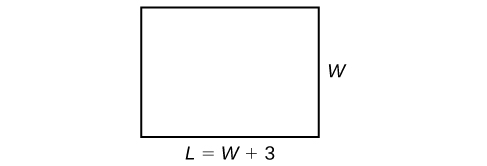
Now we can solve for the width and then calculate the length.
The dimensions are ft and ft.
Find the dimensions of a rectangle given that the perimeter is cm and the length is 1 cm more than twice the width.
cm, cm
The perimeter of a tablet of graph paper is 48 in. The length is in. more than the width. Find the area of the graph paper.
The standard formula for area is however, we will solve the problem using the perimeter formula. The reason we use the perimeter formula is because we know enough information about the perimeter that the formula will allow us to solve for one of the unknowns. As both perimeter and area use length and width as dimensions, they are often used together to solve a problem such as this one.
We know that the length is 6 in. more than the width, so we can write length as Substitute the value of the perimeter and the expression for length into the perimeter formula and find the length.
Now, we find the area given the dimensions of in. and in.
The area is in. 2 .

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?