| << Chapter < Page | Chapter >> Page > |
Find a new representation of the equation after rotating through an angle of
Find and where and
Because
and
Substitute and into
Simplify.
Write the equations with and in the standard form.
This equation is an ellipse. [link] shows the graph.
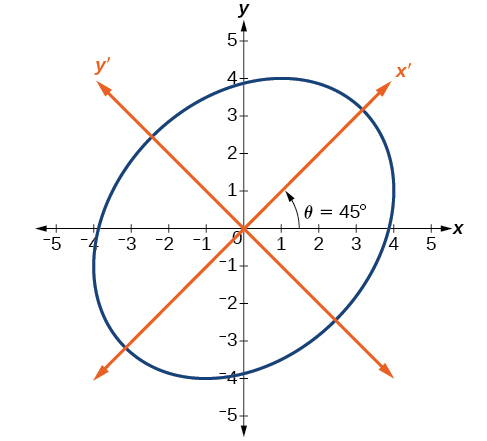
Now that we can find the standard form of a conic when we are given an angle of rotation, we will learn how to transform the equation of a conic given in the form into standard form by rotating the axes. To do so, we will rewrite the general form as an equation in the and coordinate system without the term, by rotating the axes by a measure of that satisfies
We have learned already that any conic may be represented by the second degree equation
where and are not all zero. However, if then we have an term that prevents us from rewriting the equation in standard form. To eliminate it, we can rotate the axes by an acute angle where
Given an equation for a conic in the system, rewrite the equation without the term in terms of and where the and axes are rotations of the standard axes by degrees.
Rewrite the equation in the system without an term.
First, we find See [link] .
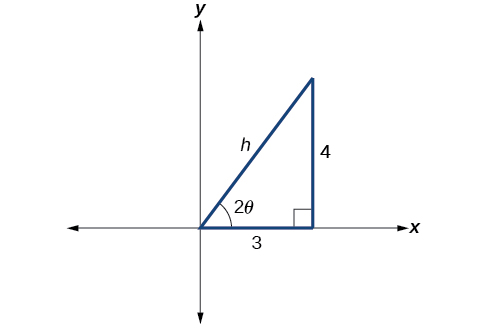
So the hypotenuse is
Next, we find and
Substitute the values of and into and
and
Substitute the expressions for and into in the given equation, and then simplify.
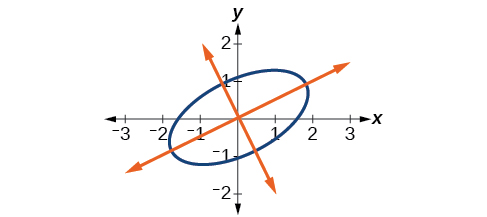
Write the equations with and in the standard form with respect to the new coordinate system.
[link] shows the graph of the ellipse.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?