12.4 Testing the significance of the correlation coefficient  (Page 4/6)

Because r is significant and the scatter plot shows a linear trend, the regression line can be used to predict final exam scores.

Assumptions in testing the significance of the correlation coefficient

Testing the significance of the correlation coefficient requires that certain assumptions about the data are satisfied. The premise of this test is that the data are a sample of observed points taken from a larger population. We have not examined the entire population because it is not possible or feasible to do so. We are examining the sample to draw a conclusion about whether the linear relationship that we see between x and y in the sample data provides strong enough evidence so that we can conclude that there is a linear relationship between x and y in the population.

The regression line equation that we calculate from the sample data gives the best-fit line for our particular sample. We want to use this best-fit line for the sample as an estimate of the best-fit line for the population. Examining the scatterplot and testing the significance of the correlation coefficient helps us determine if it is appropriate to do this.

The assumptions underlying the test of significance are:

• There is a linear relationship in the population that models the average value of y for varying values of x . In other words, the expected value of y for each particular value lies on a straight line in the population. (We do not know the equation for the line for the population. Our regression line from the sample is our best estimate of this line in the population.)
• The y values for any particular x value are normally distributed about the line. This implies that there are more y values scattered closer to the line than are scattered farther away. Assumption (1) implies that these normal distributions are centered on the line: the means of these normal distributions of y values lie on the line.
• The standard deviations of the population y values about the line are equal for each value of x . In other words, each of these normal distributions of y values has the same shape and spread about the line.
• The residual errors are mutually independent (no pattern).
• The data are produced from a well-designed, random sample or randomized experiment.

Chapter review

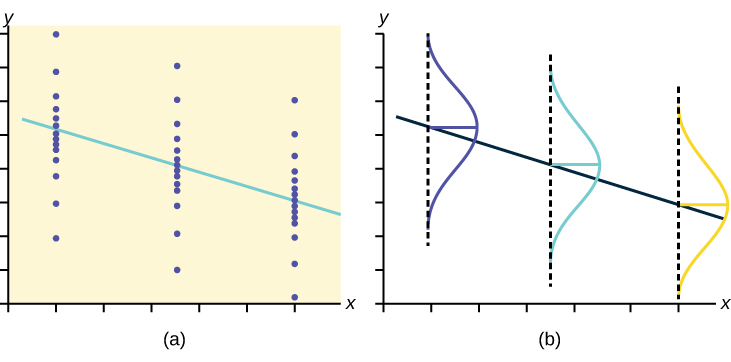
Linear regression is a procedure for fitting a straight line of the form ŷ = a + bx to data. The conditions for regression are:

• Linear In the population, there is a linear relationship that models the average value of y for different values of x .
• Independent The residuals are assumed to be independent.
• Normal The y values are distributed normally for any value of x .
• Equal variance The standard deviation of the y values is equal for each x value.
• Random The data are produced from a well-designed random sample or randomized experiment.

The slope b and intercept a of the least-squares line estimate the slope β and intercept α of the population (true) regression line. To estimate the population standard deviation of y , σ , use the standard deviation of the residuals, s . $s=\sqrt{\frac{SEE}{n-2}}$ . The variable ρ (rho) is the population correlation coefficient. To test the null hypothesis H ₀ : ρ = hypothesized value , use a linear regression t-test. The most common null hypothesis is H ₀ : ρ = 0 which indicates there is no linear relationship between x and y in the population. The TI-83, 83+, 84, 84+ calculator function LinRegTTest can perform this test (STATS TESTS LinRegTTest).

Formula review

Least Squares Line or Line of Best Fit:

$\widehat{y}=a+bx$

where

a = y -intercept

b = slope

Standard deviation of the residuals:

$s=\sqrt{\frac{SEE}{n-2}}.$

where

SSE = sum of squared errors

n = the number of data points