| << Chapter < Page | Chapter >> Page > |
In previous examples, we evaluated the sine and cosine in triangles where we knew all three sides. But the real power of right-triangle trigonometry emerges when we look at triangles in which we know an angle but do not know all the sides.
Given a right triangle, the length of one side, and the measure of one acute angle, find the remaining sides.
Find the unknown sides of the triangle in [link] .
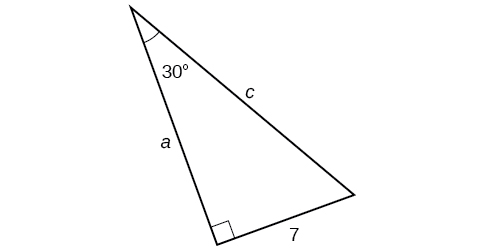
We know the angle and the opposite side, so we can use the tangent to find the adjacent side.
We rearrange to solve for
We can use the sine to find the hypotenuse.
Again, we rearrange to solve for
A right triangle has one angle of and a hypotenuse of 20. Find the unknown sides and angle of the triangle.
; missing angle is
Right-triangle trigonometry has many practical applications. For example, the ability to compute the lengths of sides of a triangle makes it possible to find the height of a tall object without climbing to the top or having to extend a tape measure along its height. We do so by measuring a distance from the base of the object to a point on the ground some distance away, where we can look up to the top of the tall object at an angle. The angle of elevation of an object above an observer relative to the observer is the angle between the horizontal and the line from the object to the observer's eye. The right triangle this position creates has sides that represent the unknown height, the measured distance from the base, and the angled line of sight from the ground to the top of the object. Knowing the measured distance to the base of the object and the angle of the line of sight, we can use trigonometric functions to calculate the unknown height. Similarly, we can form a triangle from the top of a tall object by looking downward. The angle of depression of an object below an observer relative to the observer is the angle between the horizontal and the line from the object to the observer's eye. See [link] .
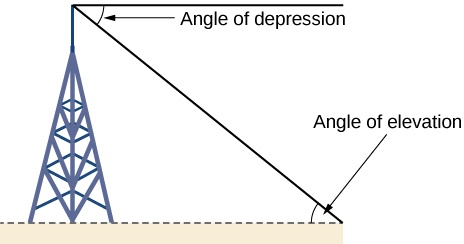
Given a tall object, measure its height indirectly.

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?