| << Chapter < Page | Chapter >> Page > |
In the previous example, the left-hand limit and right-hand limit as approaches are equal. If the left- and right-hand limits are equal, we say that the function has a two-sided limit as approaches More commonly, we simply refer to a two-sided limit as a limit. If the left-hand limit does not equal the right-hand limit, or if one of them does not exist, we say the limit does not exist.
The limit of a function as approaches is equal to that is,
if and only if
In other words, the left-hand limit of a function as approaches is equal to the right-hand limit of the same function as approaches If such a limit exists, we refer to the limit as a two-sided limit. Otherwise we say the limit does not exist.
To visually determine if a limit exists as approaches we observe the graph of the function when is very near to In [link] we observe the behavior of the graph on both sides of
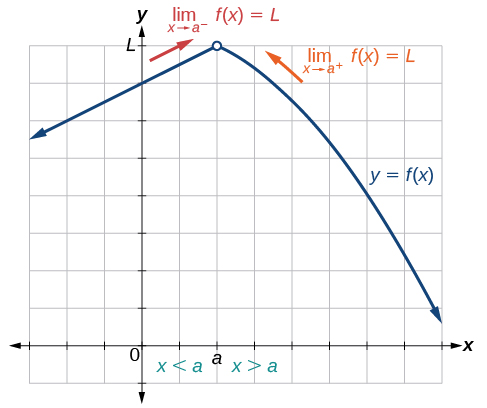
To determine if a left-hand limit exists, we observe the branch of the graph to the left of but near This is where We see that the outputs are getting close to some real number so there is a left-hand limit.
To determine if a right-hand limit exists, observe the branch of the graph to the right of but near This is where We see that the outputs are getting close to some real number so there is a right-hand limit.
If the left-hand limit and the right-hand limit are the same, as they are in [link] , then we know that the function has a two-sided limit. Normally, when we refer to a “limit,” we mean a two-sided limit, unless we call it a one-sided limit.
Finally, we can look for an output value for the function when the input value is equal to The coordinate pair of the point would be If such a point exists, then has a value. If the point does not exist, as in [link] , then we say that does not exist.
Given a function use a graph to find the limits and a function value as approaches

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?