| << Chapter < Page | Chapter >> Page > |
Do the graphs of all direct variation equations look like [link] ?
No. Direct variation equations are power functions—they may be linear, quadratic, cubic, quartic, radical, etc. But all of the graphs pass through
The quantity varies directly with the square of If when find when is 4.
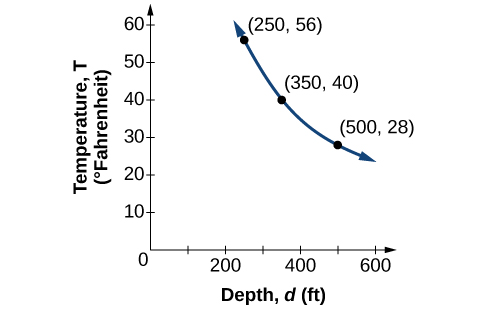
Water temperature in an ocean varies inversely to the water’s depth. Between the depths of 250 feet and 500 feet, the formula gives us the temperature in degrees Fahrenheit at a depth in feet below Earth’s surface. Consider the Atlantic Ocean, which covers 22% of Earth’s surface. At a certain location, at the depth of 500 feet, the temperature may be 28°F.
If we create [link] , we observe that, as the depth increases, the water temperature decreases.
| depth | Interpretation | |
|---|---|---|
| 500 ft | At a depth of 500 ft, the water temperature is 28° F. | |
| 350 ft | At a depth of 350 ft, the water temperature is 40° F. | |
| 250 ft | At a depth of 250 ft, the water temperature is 56° F. |
We notice in the relationship between these variables that, as one quantity increases, the other decreases. The two quantities are said to be inversely proportional and each term varies inversely with the other. Inversely proportional relationships are also called inverse variations .
For our example, [link] depicts the inverse variation . We say the water temperature varies inversely with the depth of the water because, as the depth increases, the temperature decreases. The formula for inverse variation in this case uses
If and are related by an equation of the form
where is a nonzero constant, then we say that varies inversely with the power of In inversely proportional relationships, or inverse variations , there is a constant multiple
A tourist plans to drive 100 miles. Find a formula for the time the trip will take as a function of the speed the tourist drives.
Recall that multiplying speed by time gives distance. If we let represent the drive time in hours, and represent the velocity (speed or rate) at which the tourist drives, then Because the distance is fixed at 100 miles, Solving this relationship for the time gives us our function.
We can see that the constant of variation is 100 and, although we can write the relationship using the negative exponent, it is more common to see it written as a fraction.
Given a description of an indirect variation problem, solve for an unknown.
A quantity varies inversely with the cube of If when find when is 6.
The general formula for inverse variation with a cube is The constant can be found by multiplying by the cube of
Now we use the constant to write an equation that represents this relationship.
Substitute and solve for

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?