| << Chapter < Page | Chapter >> Page > |
For the function , find the values of such that .
Should we always expect two answers when solving
No. We may find one, two, or even no answers. For example, there is no solution to
Given an absolute value equation, solve it.
Solve
Isolating the absolute value on one side of the equation gives the following.
The absolute value always returns a positive value, so it is impossible for the absolute value to equal a negative value. At this point, we notice that this equation has no solutions.
In [link] , if and were graphed on the same set of axes, would the graphs intersect?
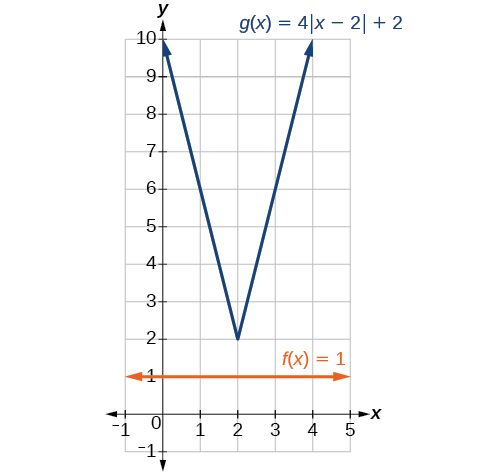
No. The graphs of and would not intersect, as shown in [link] . This confirms, graphically, that the equation has no solution.
Find where the graph of the function intersects the horizontal and vertical axes.
so the graph intersects the vertical axis at when and so the graph intersects the horizontal axis at and
Absolute value equations may not always involve equalities. Instead, we may need to solve an equation within a range of values. We would use an absolute value inequality to solve such an equation. An absolute value inequality is an equation of the form
where an expression (and possibly but not usually ) depends on a variable Solving the inequality means finding the set of all that satisfy the inequality. Usually this set will be an interval or the union of two intervals.
There are two basic approaches to solving absolute value inequalities: graphical and algebraic. The advantage of the graphical approach is we can read the solution by interpreting the graphs of two functions. The advantage of the algebraic approach is it yields solutions that may be difficult to read from the graph.
For example, we know that all numbers within 200 units of 0 may be expressed as
Suppose we want to know all possible returns on an investment if we could earn some amount of money within $200 of $600. We can solve algebraically for the set of values such that the distance between and 600 is less than 200. We represent the distance between and 600 as
This means our returns would be between $400 and $800.
Sometimes an absolute value inequality problem will be presented to us in terms of a shifted and/or stretched or compressed absolute value function, where we must determine for which values of the input the function’s output will be negative or positive.

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?