1. Home
  2. Precalculus
  3. Functions
  4. Absolute value functions

1.6 Absolute value functions  (Page 2/7)

<< Chapter < Page
  Precalculus     Page 2 / 7
Chapter >> Page >
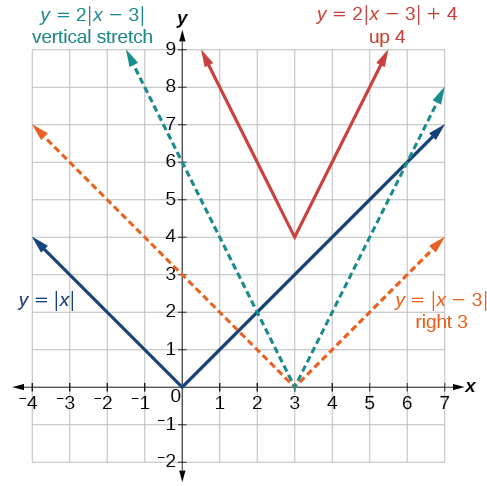
Graph of the different types of transformations for an absolute function.

Writing an equation for an absolute value function

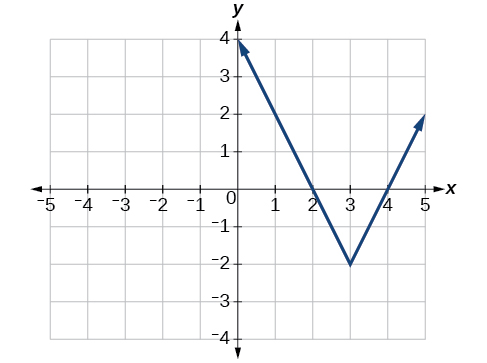
Write an equation for the function graphed in [link] .

Graph of an absolute function.

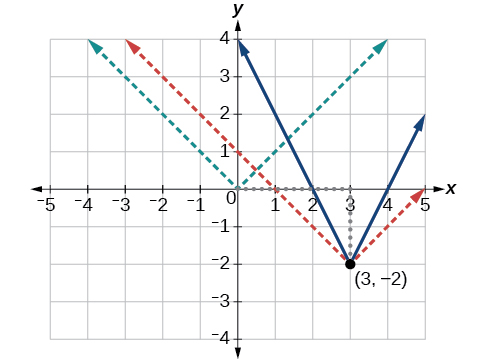
The basic absolute value function changes direction at the origin, so this graph has been shifted to the right 3 units and down 2 units from the basic toolkit function. See [link] .

Graph of two transformations for an absolute function at (3, -2).

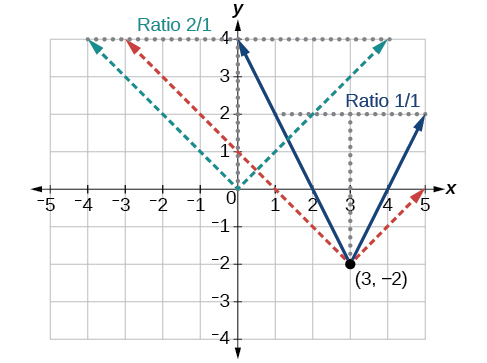
We also notice that the graph appears vertically stretched, because the width of the final graph on a horizontal line is not equal to 2 times the vertical distance from the corner to this line, as it would be for an unstretched absolute value function. Instead, the width is equal to 1 times the vertical distance as shown in [link] .

Graph of two transformations for an absolute function at (3, -2) and describes the ratios between the two different transformations.

From this information we can write the equation

f ( x ) = 2 | x − 3 | − 2 , treating the stretch as a vertical stretch, or f ( x ) = | 2 ( x − 3 ) | − 2 , treating the stretch as a horizontal compression .
Got questions? Get instant answers now!
Got questions? Get instant answers now!

If we couldn’t observe the stretch of the function from the graphs, could we algebraically determine it?

Yes. If we are unable to determine the stretch based on the width of the graph, we can solve for the stretch factor by putting in a known pair of values for   x   and   f ( x ) .

f ( x ) = a | x − 3 | − 2

Now substituting in the point (1, 2)

2 = a | 1 − 3 | − 2 4 = 2 a a = 2

Write the equation for the absolute value function that is horizontally shifted left 2 units, is vertically flipped, and vertically shifted up 3 units.

f ( x ) = − | x + 2 | + 3

Got questions? Get instant answers now!

Do the graphs of absolute value functions always intersect the vertical axis? The horizontal axis?

Yes, they always intersect the vertical axis. The graph of an absolute value function will intersect the vertical axis when the input is zero.

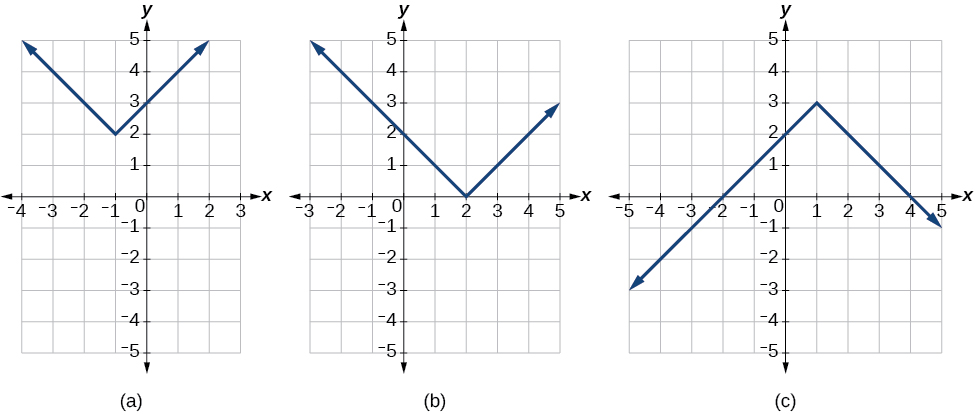
No, they do not always intersect the horizontal axis. The graph may or may not intersect the horizontal axis, depending on how the graph has been shifted and reflected. It is possible for the absolute value function to intersect the horizontal axis at zero, one, or two points (see [link] ).

Graph of the different types of transformations for an absolute function.
(a) The absolute value function does not intersect the horizontal axis. (b) The absolute value function intersects the horizontal axis at one point. (c) The absolute value function intersects the horizontal axis at two points.

Solving an absolute value equation

Now that we can graph an absolute value function, we will learn how to solve an absolute value equation. To solve an equation such as   8 = | 2 x − 6 | ,   we notice that the absolute value will be equal to 8 if the quantity inside the absolute value is 8 or -8. This leads to two different equations we can solve independently.

2 x − 6 = 8 or 2 x − 6 = − 8                 2 x = 14                   2 x = − 2                       x = 7                         x = − 1

Knowing how to solve problems involving absolute value functions is useful. For example, we may need to identify numbers or points on a line that are at a specified distance from a given reference point.

An absolute value equation    is an equation in which the unknown variable appears in absolute value bars. For example,

| x | = 4 , | 2 x − 1 | = 3 | 5 x + 2 | − 4 = 9

Solutions to absolute value equations

For real numbers   A   and   B ,   an equation of the form   | A | = B ,   with   B ≥ 0 ,   will have solutions when   A = B   or   A = − B .   If   B < 0 ,   the equation   | A | = B   has no solution.

Given the formula for an absolute value function, find the horizontal intercepts of its graph .

  1. Isolate the absolute value term.
  2. Use   | A | = B   to write   A = B   or   −A = B ,   assuming   B > 0.
  3. Solve for   x .  
<< Chapter < Page Page > Chapter >>
Practice Key Terms 2

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Precalculus. OpenStax CNX. Jan 19, 2016 Download for free at https://legacy.cnx.org/content/col11667/1.6
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Precalculus' conversation and receive update notifications?

Ask