| << Chapter < Page | Chapter >> Page > |
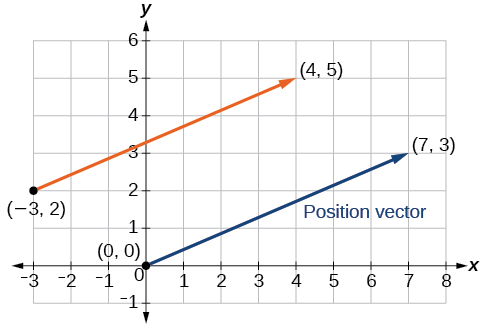
Find the position vector given that vector has an initial point at and a terminal point at then graph both vectors in the same plane.
The position vector is found using the following calculation:
Thus, the position vector begins at and terminates at See [link] .
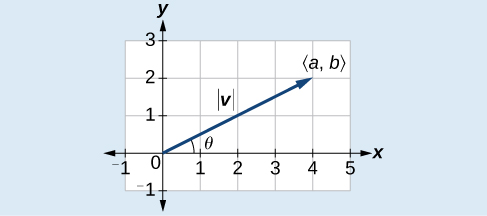
To work with a vector, we need to be able to find its magnitude and its direction. We find its magnitude using the Pythagorean Theorem or the distance formula, and we find its direction using the inverse tangent function.
Given a position vector the magnitude is found by The direction is equal to the angle formed with the x -axis, or with the y -axis, depending on the application. For a position vector, the direction is found by as illustrated in [link] .
Two vectors v and u are considered equal if they have the same magnitude and the same direction. Additionally, if both vectors have the same position vector, they are equal.
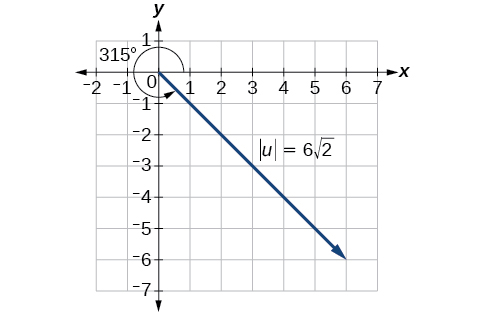
Find the magnitude and direction of the vector with initial point and terminal point Draw the vector.
First, find the position vector .
We use the Pythagorean Theorem to find the magnitude.
The direction is given as
However, the angle terminates in the fourth quadrant, so we add 360° to obtain a positive angle. Thus, See [link] .
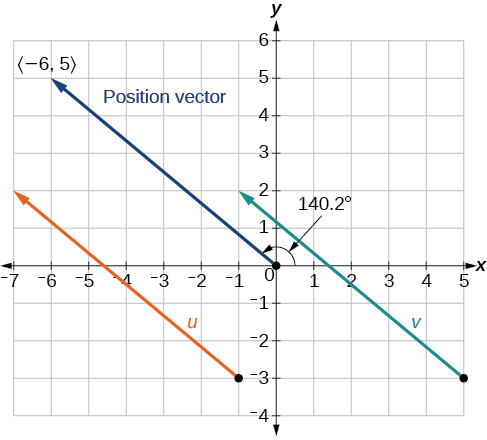
Show that vector v with initial point at and terminal point at is equal to vector u with initial point at and terminal point at Draw the position vector on the same grid as v and u . Next, find the magnitude and direction of each vector.
As shown in [link] , draw the vector starting at initial and terminal point Draw the vector with initial point and terminal point Find the standard position for each.
Next, find and sketch the position vector for v and u . We have
Since the position vectors are the same, v and u are the same.
An alternative way to check for vector equality is to show that the magnitude and direction are the same for both vectors. To show that the magnitudes are equal, use the Pythagorean Theorem.
As the magnitudes are equal, we now need to verify the direction. Using the tangent function with the position vector gives
However, we can see that the position vector terminates in the second quadrant, so we add Thus, the direction is
Now that we understand the properties of vectors, we can perform operations involving them. While it is convenient to think of the vector as an arrow or directed line segment from the origin to the point vectors can be situated anywhere in the plane. The sum of two vectors u and v , or vector addition , produces a third vector u + v , the resultant vector.

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?