| << Chapter < Page | Chapter >> Page > |
For the following exercises, use the graphs of shown in [link] , and shown in [link] , to evaluate the expressions.
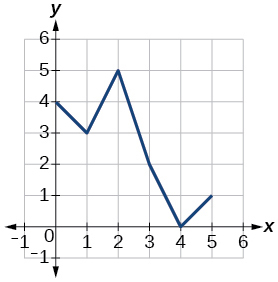
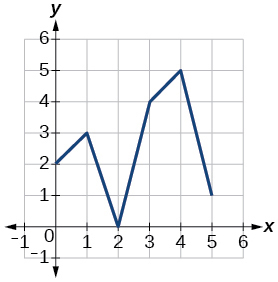
For the following exercises, use graphs of shown in [link] , shown in [link] , and shown in [link] , to evaluate the expressions.
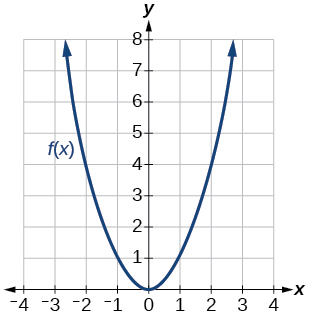
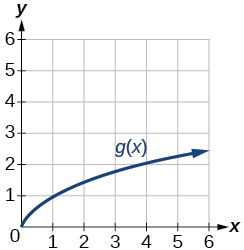
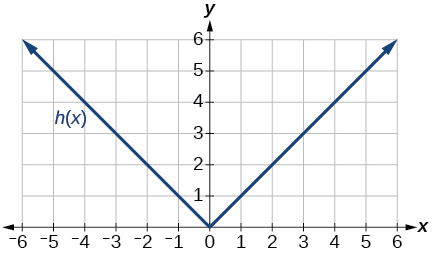
For the following exercises, use the function values for shown in [link] to evaluate each expression.
| 0 | 7 | 9 |
| 1 | 6 | 5 |
| 2 | 5 | 6 |
| 3 | 8 | 2 |
| 4 | 4 | 1 |
| 5 | 0 | 8 |
| 6 | 2 | 7 |
| 7 | 1 | 3 |
| 8 | 9 | 4 |
| 9 | 3 | 0 |
For the following exercises, use the function values for shown in [link] to evaluate the expressions.
| -3 | 11 | -8 |
| -2 | 9 | -3 |
| -1 | 7 | 0 |
| 0 | 5 | 1 |
| 1 | 3 | 0 |
| 2 | 1 | -3 |
| 3 | -1 | -8 |
For the following exercises, use each pair of functions to find and
For the following exercises, use the functions and to evaluate or find the composite function as indicated.
For the following exercises, use and
Find and Compare the two answers.
What is the domain of
Let
For the following exercises, let and
True or False:
For the following exercises, find the composition when for all and
The function gives the number of items that will be demanded when the price is The production cost is the cost of producing items. To determine the cost of production when the price is $6, you would do which of the following?
The function gives the pain level on a scale of 0 to 10 experienced by a patient with milligrams of a pain-reducing drug in her system. The milligrams of the drug in the patient’s system after minutes is modeled by Which of the following would you do in order to determine when the patient will be at a pain level of 4?
c
A store offers customers a 30% discount on the price of selected items. Then, the store takes off an additional 15% at the cash register. Write a price function that computes the final price of the item in terms of the original price (Hint: Use function composition to find your answer.)
A rain drop hitting a lake makes a circular ripple. If the radius, in inches, grows as a function of time in minutes according to find the area of the ripple as a function of time. Find the area of the ripple at
and square inches
A forest fire leaves behind an area of grass burned in an expanding circular pattern. If the radius of the circle of burning grass is increasing with time according to the formula express the area burned as a function of time, (minutes).
Use the function you found in the previous exercise to find the total area burned after 5 minutes.
square units
The radius in inches, of a spherical balloon is related to the volume, by Air is pumped into the balloon, so the volume after seconds is given by
The number of bacteria in a refrigerated food product is given by where is the temperature of the food. When the food is removed from the refrigerator, the temperature is given by where is the time in hours.
a. b. 3.38 hours

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?