| << Chapter < Page | Chapter >> Page > |
We cannot plot complex numbers on a number line as we might real numbers. However, we can still represent them graphically. To represent a complex number we need to address the two components of the number. We use the complex plane , which is a coordinate system in which the horizontal axis represents the real component and the vertical axis represents the imaginary component. Complex numbers are the points on the plane, expressed as ordered pairs where represents the coordinate for the horizontal axis and represents the coordinate for the vertical axis.
Let’s consider the number The real part of the complex number is and the imaginary part is We plot the ordered pair to represent the complex number as shown in [link] .
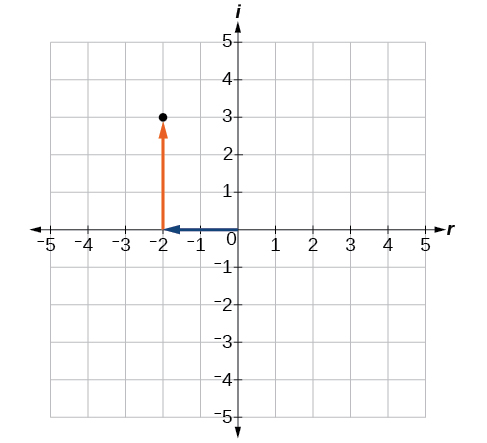
In the complex plane , the horizontal axis is the real axis, and the vertical axis is the imaginary axis as shown in [link] .
Given a complex number, represent its components on the complex plane.
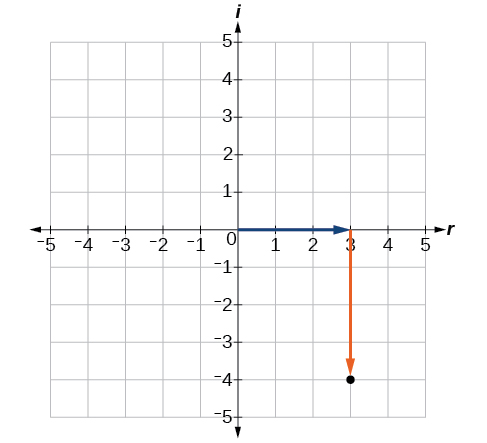
Plot the complex number on the complex plane.
The real part of the complex number is and the imaginary part is We plot the ordered pair as shown in [link] .
Just as with real numbers, we can perform arithmetic operations on complex numbers. To add or subtract complex numbers, we combine the real parts and combine the imaginary parts.
Adding complex numbers:
Subtracting complex numbers:
Given two complex numbers, find the sum or difference.
Add and
We add the real parts and add the imaginary parts.
Multiplying complex numbers is much like multiplying binomials. The major difference is that we work with the real and imaginary parts separately.
Let’s begin by multiplying a complex number by a real number. We distribute the real number just as we would with a binomial. So, for example,
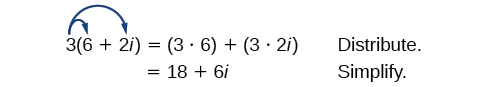
Given a complex number and a real number, multiply to find the product.
Find the product
Distribute the 4.

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?