-
Home
- Precalculus
- Functions
- Functions and function notation
We will see these toolkit functions, combinations of toolkit functions, their graphs, and their transformations frequently throughout this book. It will be very helpful if we can recognize these toolkit functions and their features quickly by name, formula, graph, and basic table properties. The graphs and sample table values are included with each function shown in
[link] .
| Toolkit Functions |
| Name |
Function |
Graph |
| Constant |
where
is a constant |
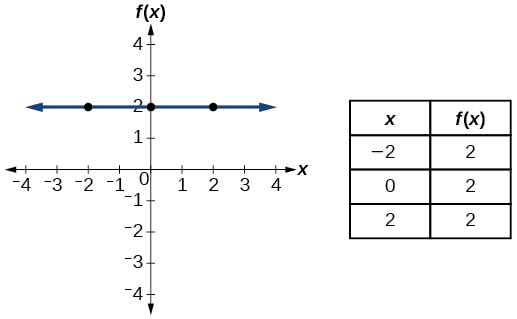 |
| Identity |
|
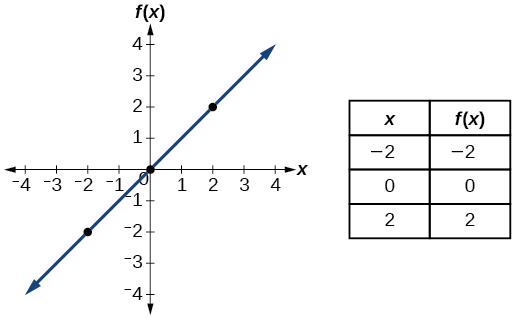 |
| Absolute value |
|
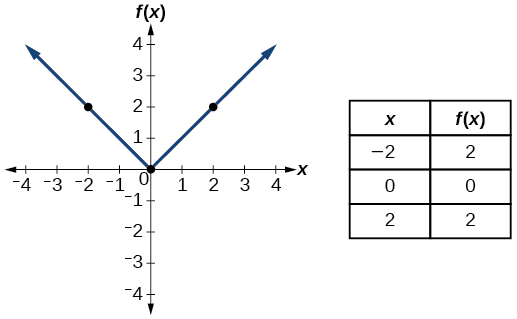 |
| Quadratic |
|
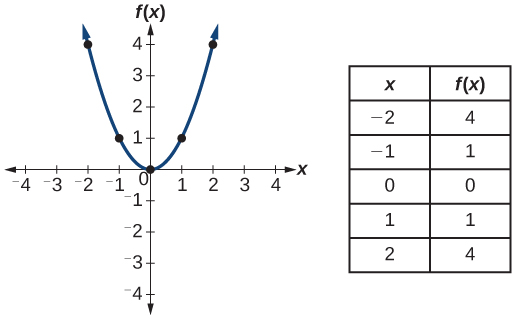 |
| Cubic |
|
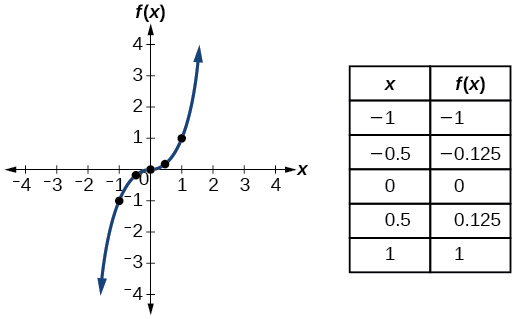 |
| Reciprocal |
|
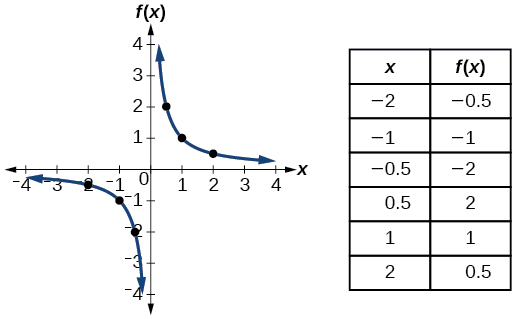 |
| Reciprocal squared |
|
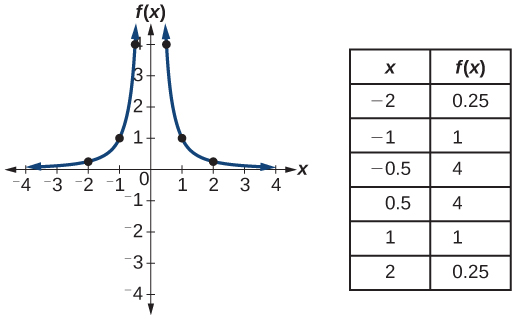 |
| Square root |
|
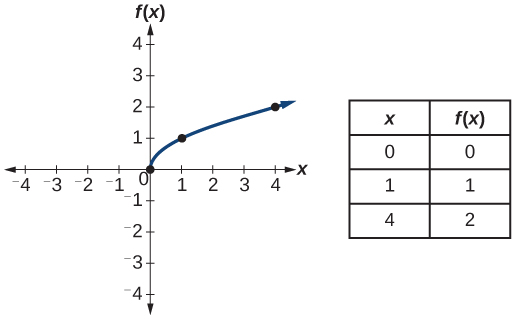 |
| Cube root |
|
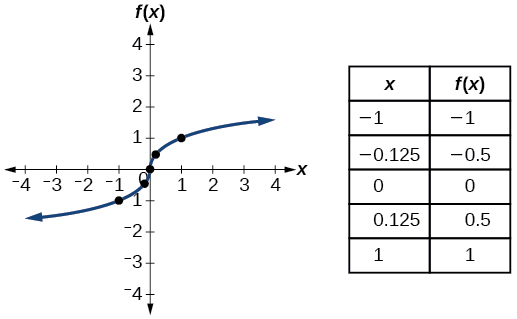 |
Key equations
| Constant function |
where
is a constant |
| Identity function |
|
| Absolute value function |
|
| Quadratic function |
|
| Cubic function |
|
| Reciprocal function |
|
| Reciprocal squared function |
|
| Square root function |
|
| Cube root function |
|
Key concepts
- A relation is a set of ordered pairs. A function is a specific type of relation in which each domain value, or input, leads to exactly one range value, or output. See
[link] and
[link] .
- Function notation is a shorthand method for relating the input to the output in the form
See
[link] and
[link] .
- In tabular form, a function can be represented by rows or columns that relate to input and output values. See
[link] .
- To evaluate a function, we determine an output value for a corresponding input value. Algebraic forms of a function can be evaluated by replacing the input variable with a given value. See
[link] and
[link] .
- To solve for a specific function value, we determine the input values that yield the specific output value. See
[link] .
- An algebraic form of a function can be written from an equation. See
[link] and
[link] .
- Input and output values of a function can be identified from a table. See
[link] .
- Relating input values to output values on a graph is another way to evaluate a function. See
[link] .
- A function is one-to-one if each output value corresponds to only one input value. See
[link] .
- A graph represents a function if any vertical line drawn on the graph intersects the graph at no more than one point. See
[link] .
- The graph of a one-to-one function passes the horizontal line test. See
[link] .
Section exercises
Verbal
What is the difference between a relation and a function?
A relation is a set of ordered pairs. A function is a special kind of relation in which no two ordered pairs have the same first coordinate.
Got questions? Get instant answers now!
Why does the vertical line test tell us whether the graph of a relation represents a function?
When a vertical line intersects the graph of a relation more than once, that indicates that for that input there is more than one output. At any particular input value, there can be only one output if the relation is to be a function.
Got questions? Get instant answers now!
Questions & Answers
A golfer on a fairway is 70 m away from the green, which sits below the level of the fairway by 20 m. If the golfer hits the ball at an angle of 40° with an initial speed of 20 m/s, how close to the green does she come?
A mouse of mass 200 g falls 100 m down a vertical mine shaft and lands at the bottom with a speed of 8.0 m/s. During its fall, how much work is done on the mouse by air resistance
Can you compute that for me. Ty
Jude
what is the dimension formula of energy?
Chemistry is a branch of science that deals with the study of matter,it composition,it structure and the changes it undergoes
Adjei
please, I'm a physics student and I need help in physics
Adjanou
chemistry could also be understood like the sexual attraction/repulsion of the male and female elements. the reaction varies depending on the energy differences of each given gender. + masculine -female.
Pedro
A ball is thrown straight up.it passes a 2.0m high window 7.50 m off the ground on it path up and takes 1.30 s to go past the window.what was the ball initial velocity
2. A sled plus passenger with total mass 50 kg is pulled 20 m across the snow (0.20) at constant velocity by a force directed 25° above the horizontal. Calculate (a) the work of the applied force, (b) the work of friction, and (c) the total work.
you have been hired as an espert witness in a court case involving an automobile accident. the accident involved car A of mass 1500kg which crashed into stationary car B of mass 1100kg. the driver of car A applied his brakes 15 m before he skidded and crashed into car B. after the collision, car A s
can someone explain to me, an ignorant high school student, why the trend of the graph doesn't follow the fact that the higher frequency a sound wave is, the more power it is, hence, making me think the phons output would follow this general trend?
Nevermind i just realied that the graph is the phons output for a person with normal hearing and not just the phons output of the sound waves power, I should read the entire thing next time
Joseph
Follow up question, does anyone know where I can find a graph that accuretly depicts the actual relative "power" output of sound over its frequency instead of just humans hearing
Joseph
"Generation of electrical energy from sound energy | IEEE Conference Publication | IEEE Xplore" ***ieeexplore.ieee.org/document/7150687?reload=true
Ryan
what are the types of wave
Maurice
fine, how about you?
Mohammed
A string is 3.00 m long with a mass of 5.00 g. The string is held taut with a tension of 500.00 N applied to the string. A pulse is sent down the string. How long does it take the pulse to travel the 3.00 m of the string?
Who can show me the full solution in this problem?
Got questions? Join the online conversation and get instant answers!
Source:
OpenStax, Precalculus. OpenStax CNX. Jan 19, 2016 Download for free at https://legacy.cnx.org/content/col11667/1.6
Google Play and the Google Play logo are trademarks of Google Inc.









