| << Chapter < Page | Chapter >> Page > |
Given the polar equation for a conic, identify the type of conic, the directrix, and the eccentricity.
For each of the following equations, identify the conic with focus at the origin, the directrix , and the eccentricity .
For each of the three conics, we will rewrite the equation in standard form. Standard form has a 1 as the constant in the denominator. Therefore, in all three parts, the first step will be to multiply the numerator and denominator by the reciprocal of the constant of the original equation, where is that constant.
Because is in the denominator, the directrix is Comparing to standard form, note that Therefore, from the numerator,
Since the conic is an ellipse . The eccentricity is and the directrix is
Because is in the denominator, the directrix is Comparing to standard form, Therefore, from the numerator,
Since the conic is a hyperbola . The eccentricity is and the directrix is
Because sine is in the denominator, the directrix is Comparing to standard form, Therefore, from the numerator,
Because the conic is a parabola . The eccentricity is and the directrix is
Identify the conic with focus at the origin, the directrix, and the eccentricity for
ellipse;
When graphing in Cartesian coordinates, each conic section has a unique equation. This is not the case when graphing in polar coordinates. We must use the eccentricity of a conic section to determine which type of curve to graph, and then determine its specific characteristics. The first step is to rewrite the conic in standard form as we have done in the previous example. In other words, we need to rewrite the equation so that the denominator begins with 1. This enables us to determine and, therefore, the shape of the curve. The next step is to substitute values for and solve for to plot a few key points. Setting equal to and provides the vertices so we can create a rough sketch of the graph.
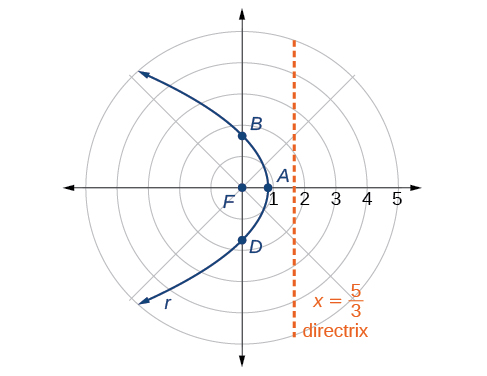
Graph
First, we rewrite the conic in standard form by multiplying the numerator and denominator by the reciprocal of 3, which is
Because we will graph a parabola with a focus at the origin. The function has a and there is an addition sign in the denominator, so the directrix is
The directrix is
Plotting a few key points as in [link] will enable us to see the vertices. See [link] .
| A | B | C | D | |
|---|---|---|---|---|
| undefined |

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?