| << Chapter < Page | Chapter >> Page > |
When working with right triangles, the same rules apply regardless of the orientation of the triangle. In fact, we can evaluate the six trigonometric functions of either of the two acute angles in the triangle in [link] . The side opposite one acute angle is the side adjacent to the other acute angle, and vice versa.
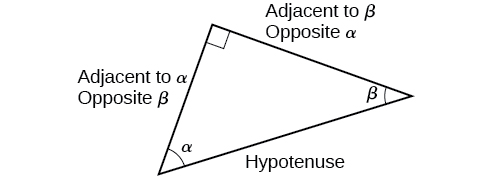
We will be asked to find all six trigonometric functions for a given angle in a triangle. Our strategy is to find the sine, cosine, and tangent of the angles first. Then, we can find the other trigonometric functions easily because we know that the reciprocal of sine is cosecant, the reciprocal of cosine is secant, and the reciprocal of tangent is cotangent.
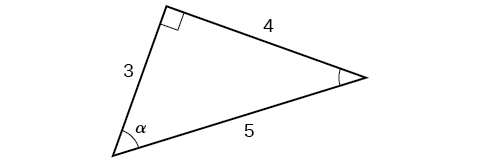
Given the side lengths of a right triangle, evaluate the six trigonometric functions of one of the acute angles.
Using the triangle shown in [link] , evaluate and
We have already discussed the trigonometric functions as they relate to the special angles on the unit circle. Now, we can use those relationships to evaluate triangles that contain those special angles. We do this because when we evaluate the special angles in trigonometric functions, they have relatively friendly values, values that contain either no or just one square root in the ratio. Therefore, these are the angles often used in math and science problems. We will use multiples of and however, remember that when dealing with right triangles, we are limited to angles between
Suppose we have a triangle, which can also be described as a triangle. The sides have lengths in the relation The sides of a triangle, which can also be described as a triangle, have lengths in the relation These relations are shown in [link] .
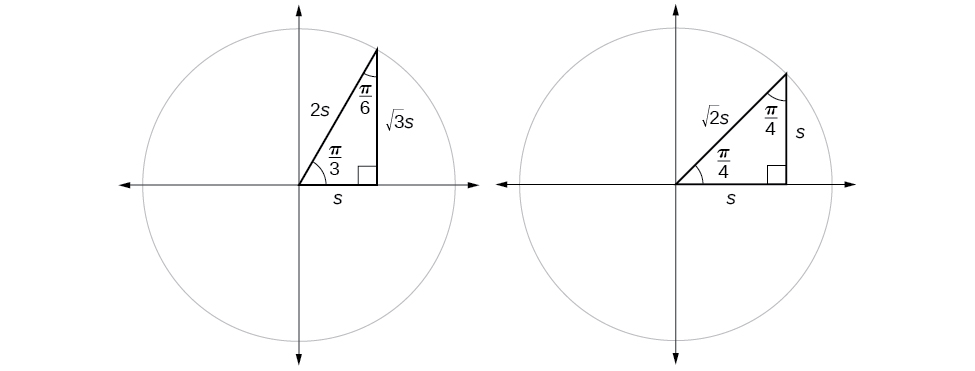
We can then use the ratios of the side lengths to evaluate trigonometric functions of special angles.

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?