5.1 Angles  (Page 5/29)

Finding coterminal angles

Converting between degrees and radians can make working with angles easier in some applications. For other applications, we may need another type of conversion. Negative angles and angles greater than a full revolution are more awkward to work with than those in the range of 0° to 360°, or 0 to $2\pi .$ It would be convenient to replace those out-of-range angles with a corresponding angle within the range of a single revolution.

It is possible for more than one angle to have the same terminal side. Look at [link] . The angle of 140° is a positive angle    , measured counterclockwise. The angle of –220° is a negative angle    , measured clockwise. But both angles have the same terminal side. If two angles in standard position have the same terminal side, they are coterminal angles    . Every angle greater than 360° or less than 0° is coterminal with an angle between 0° and 360°, and it is often more convenient to find the coterminal angle within the range of 0° to 360° than to work with an angle that is outside that range.

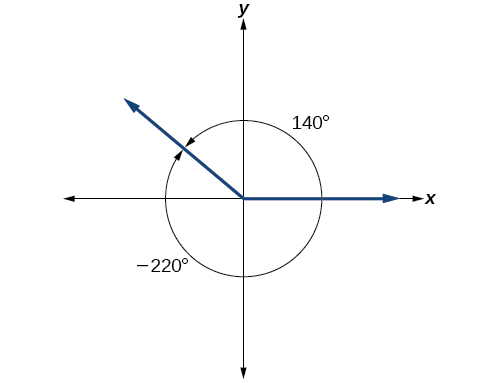
Any angle has infinitely many coterminal angles    because each time we add 360° to that angle—or subtract 360° from it—the resulting value has a terminal side in the same location. For example, 100° and 460° are coterminal for this reason, as is −260°. Recognizing that any angle has infinitely many coterminal angles explains the repetitive shape in the graphs of trigonometric functions.

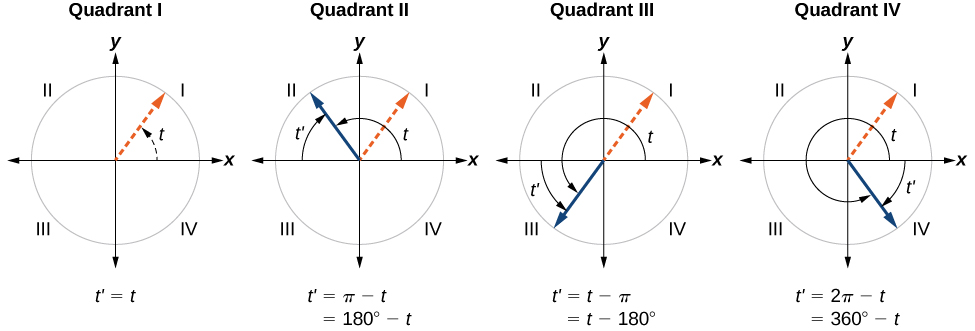
An angle’s reference angle is the measure of the smallest, positive, acute angle $t$ formed by the terminal side of the angle $t$ and the horizontal axis. Thus positive reference angles have terminal sides that lie in the first quadrant and can be used as models for angles in other quadrants. See [link] for examples of reference angles for angles in different quadrants.

Finding an angle coterminal with an angle of measure greater than 360°

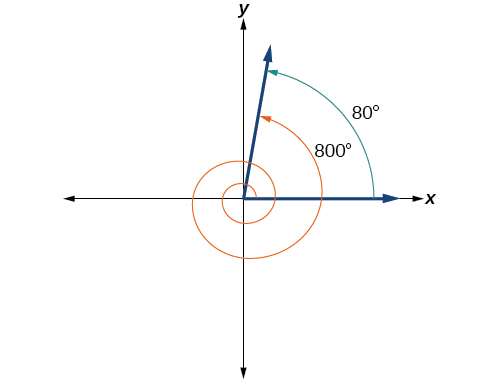
Find the least positive angle $\theta$ that is coterminal with an angle measuring 800°, where $\mathrm{0°}\le \theta <\mathrm{360°}.$

An angle with measure 800° is coterminal with an angle with measure 800 − 360 = 440°, but 440° is still greater than 360°, so we subtract 360° again to find another coterminal angle: 440 − 360 = 80°.

The angle $\theta =\mathrm{80°}$ is coterminal with 800°. To put it another way, 800° equals 80° plus two full rotations, as shown in [link] .

Got questions? Get instant answers now!

Got questions? Get instant answers now!